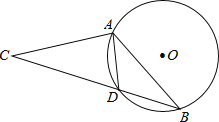
【题目】如图,在⊙O中,弦AD等于半径,B为优弧AD上的一动点,等腰△ABC的底边BC所在直线经过点D.若⊙O的半径等于1,则OC的长不可能为( )
A.2﹣![]() B.
B.![]() ﹣1 C.2 D.
﹣1 C.2 D.![]() +1
+1
参考答案:
【答案】A
【解析】
试题分析:利用圆周角定理确定点C的运动轨迹,进而利用点与圆的位置关系求得OC长度的取值范围.
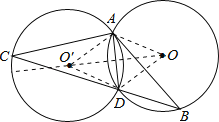
解:如图,连接OA、OD,则△OAD为等边三角形,边长为半径1.
作点O关于AD的对称点O′,连接O′A、O′D,则△O′AD也是等边三角形,边长为半径1,
∴OO′=![]() ×2=
×2=![]() .
.
由题意可知,∠ACB=∠ABC=![]() ∠AOD=30°,
∠AOD=30°,
∴∠ACB=![]() ∠AO′D,
∠AO′D,
∴点C在半径为1的⊙O′上运动.
由图可知,OC长度的取值范围是:![]() ﹣1≤OC≤
﹣1≤OC≤![]() +1.
+1.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC∽△DEF,相似比为3:5,△ABC的周长为6,则△DEF的周长为.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知2a3mb和 - 2a6bn+2是同类项,化简并求值:2(m2 - mn) - 3(2m2 - 3mn) - 2[m2 - (2m2 - mn+m2)] - 1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB、BC、AC三边的长分别为
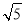 、
、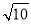 、
、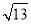 ,求这个三角形的面积小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求这个三角形的面积小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.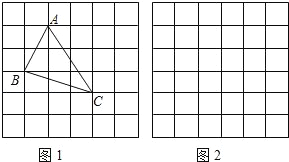
(1)请你将△ABC的面积直接填写在横线上
(2)画△DEF,DE、EF、DF三边的长分别为
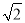 、
、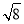 、
、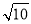
①判断三角形的形状,说明理由.
②求这个三角形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业新增了一个化工项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共8台,具体情况如下表:
A型
B型
价格(万元/台)
12
10
月污水处理能力(吨/月)
200
160
经预算,企业最多支出89万元购买设备,且要求月处理污水能力不低于1380吨.
(1)该企业有几种购买方案?
(2)哪种方案更省钱,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品的价格标签已丢失,售货员只知道“它的进价为80元,打七折售出后,仍可获利4元”,你认为售货员应标在标签上的价格是______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x1,x2是一元二次方程x2﹣2x﹣1=0的两个根,则x12﹣x1+x2的值为( )
A.﹣1 B.0 C.2 D.3
相关试题

