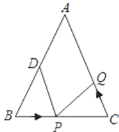
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1s后,BP= cm,CQ= cm.
(2)若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
(3)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(4)若点Q以(3)中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次相遇?
参考答案:
【答案】(1)BP=3cm,CQ=3cm;(2)全等,理由详见解析;(3)![]() ;(4)经过
;(4)经过![]() s点P与点Q第一次相遇.
s点P与点Q第一次相遇.
【解析】
(1)速度和时间相乘可得BP、CQ的长;
(2)利用SAS可证三角形全等;
(3)三角形全等,则可得出BP=PC,CQ=BD,从而求出t的值;
(4)第一次相遇,即点Q第一次追上点P,即点Q的运动的路程比点P运动的路程多10+10=20cm的长度.
解:(1)BP=3×1=3㎝,
CQ=3×1=3㎝
(2)∵t=1s,点Q的运动速度与点P的运动速度相等
∴BP=CQ=3×1=3cm,
∵AB=10cm,点D为AB的中点,
∴BD=5cm.
又∵PC=BC﹣BP,BC=8cm,
∴PC=8﹣3=5cm,
∴PC=BD
又∵AB=AC,
∴∠B=∠C,
在△BPD和△CQP中,
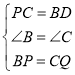
∴△BPD≌△CQP(SAS)
(3)∵点Q的运动速度与点P的运动速度不相等,
∴BP与CQ不是对应边,
即BP≠CQ
∴若△BPD≌△CPQ,且∠B=∠C,
则BP=PC=4cm,CQ=BD=5cm,
∴点P,点Q运动的时间t=![]() s,
s,
∴![]() cm/s;
cm/s;
(4)设经过x秒后点P与点Q第一次相遇.
由题意,得![]() x=3x+2×10,
x=3x+2×10,
解得![]()
∴经过![]() s点P与点Q第一次相遇.
s点P与点Q第一次相遇.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C是⊙O上的一点,DA与⊙O相切于点A,DA=DC=
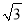 .
.
(1)求证:DC是⊙O的切线;
(2)若∠CAB=30°,求阴影部分的面积.
-
科目: 来源: 题型:
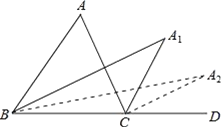
查看答案和解析>>【题目】如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2015BC和∠A20l5CD的平分线交于点A2016,则∠A2016=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形ABCD中,AD∥BC,∠A=90°,BD⊥CD,垂足为D.
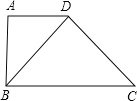
(1)若AD=9,BC=16,求BD的长;
(2)求证:AB2BC=CD2AD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△DEB中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是

A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
-
科目: 来源: 题型:
查看答案和解析>>【题目】某相宜本草护肤品专柜计划在春节前夕促销甲、乙两款护肤品,根据市场调研,发现如下两种信息:
信息一:销售甲款护肤品所获利润y(元)与销售量x(件)之间存在二次函数关系y=ax2+bx.在x=10时,y=140;当x=30时,y=360.
信息二:销售乙款护肤品所获利润y(元)与销售量x(件)之间存在正比例函数关系y=3x.请根据以上信息,解答下列问题;
(1)求信息一中二次函数的表达式;
(2)该相宜本草护肤品专柜计划在春节前夕促销甲、乙两款护肤品共100件,请设计一个营销方案,使销售甲、乙两款护肤品获得的利润之和最大,并求出最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(
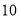 分)如图,某幼儿园为了加强安全管理,决定将园内的滑滑板的倾角由
分)如图,某幼儿园为了加强安全管理,决定将园内的滑滑板的倾角由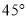 降为
降为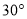 ,已知
,已知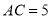 米,点
米,点 ,
, 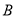 ,
, 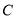 在同一水平地面上,
在同一水平地面上, 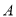 ,
,  ,
,  ,
,  在同一平面内.
在同一平面内.(
 )求改善后滑滑板
)求改善后滑滑板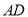 的长.
的长.(
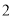 )若滑滑板的正前方有
)若滑滑板的正前方有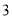 米长的空地就能保证安全,原滑滑板的前方有
米长的空地就能保证安全,原滑滑板的前方有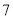 米长的空地,这样改善方案是否可行?说明理由.
米长的空地,这样改善方案是否可行?说明理由.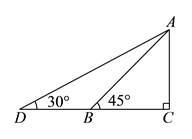
(
 )∵在
)∵在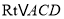 中,
中, 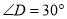 ,
,∴
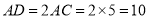 米.
米.(或:∵在
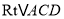 中,
中, 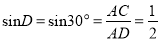 ,∴
,∴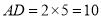 米).
米).答:改善后
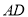 长
长 米.
米.(
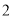 )∵在
)∵在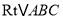 中,
中, 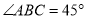 ,
,∴
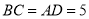 米,
米,∵在
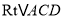 中,
中, 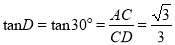 ,
,∴
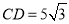 米,
米,∴
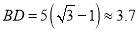 米,
米,∵
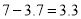 米,
米, 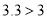 ,
,∴这样的改善方案可行.
相关试题

