【题目】如图,抛物线y=ax2+bx+c(a≠0)的图象经过点A,B,C,已知点A的坐标为(﹣3,0),点B坐标为(1,0),点C在y轴的正半轴,且∠CAB=30°.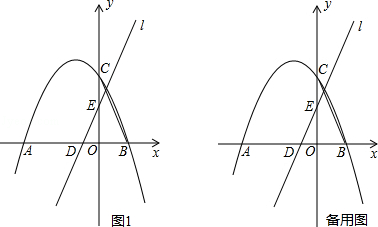
(1)求抛物线的函数解析式;
(2)若直线l:y= ![]() x+m从点C开始沿y轴向下平移,分别交x轴、y轴于点D、E.
x+m从点C开始沿y轴向下平移,分别交x轴、y轴于点D、E.
①当m>0时,在线段AC上否存在点P,使得点P,D,E构成等腰直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
②以动直线l为对称轴,线段AC关于直线l的对称线段A′C′与二次函数图象有交点,请直接写出m的取值范围.
参考答案:
【答案】
(1)
解:如图1,连结AC,在Rt△AOC中,∠CAB=30°,
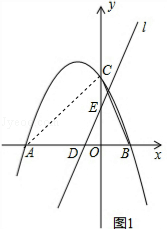
∵A(﹣3,0),即OA=3,
∴OC= ![]() ,即C(0,
,即C(0, ![]() ),
),
设抛物线解析式为 ![]() ,
,
将A(﹣3,0),B(1,0)代入得 ![]() .
.
解得 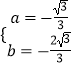 .
.
∴ ![]()
(2)
解:由题意可知,OE=m,OD= ![]() ,∠DEO=30°,
,∠DEO=30°,
(i)如图2,当PD⊥DE,DP=DE,作PQ⊥x轴
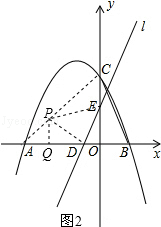
∴∠PQD=∠EOD=90°,
∠PDQ+∠EDO=90°,∠EDO+∠DEO=90°,
∴∠DEO=∠PDQ=30°,
在△DPQ与△EDO中,
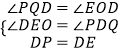 ,
,
∴△DPQ≌△EDO(AAS),
∴DQ=OE=m,
∵∠PAQ=∠PDQ=30°,
∴PA=PD,
∴AQ=DQ=m,
∴OA=2m+ ![]() =3,
=3,
∴ ![]() ;
;
(ii)如图3,当PE⊥DE,PE=DE,作PQ⊥y轴,
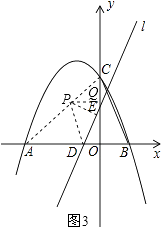
同理可得CQ=EQ=OD= ![]() ,
,
∴OC=m+ ![]() =
= ![]() ,
,
∴ ![]() ;
;
(iii)如图4,当DP⊥PE,DP=PE,作DM⊥AC,EN⊥AC,
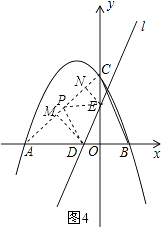
同理可得AP=AD= ![]() ,PN=DM=
,PN=DM= ![]() ,CN=
,CN= ![]()
∴AC= ![]() +
+ ![]() +
+ ![]() =
= ![]() ,
,
∴ ![]() ;
;
②当x=0,y= ![]() 时,
时, ![]() =0+m,解得m=
=0+m,解得m= ![]() ;
;
当x=0,y=﹣ ![]() 时,﹣
时,﹣ ![]() =0+m,解得m=﹣
=0+m,解得m=﹣ ![]() .
.
故m的取值范围为: ![]()
【解析】(1)如图1,连结AC,在Rt△AOC中,∠CAB=30°,根据三角函数可得C(0, ![]() ),根据待定系数法可求抛物线解析式;(2)①由题意可知,OE=m,OD=
),根据待定系数法可求抛物线解析式;(2)①由题意可知,OE=m,OD= ![]() ,∠DEO=30°,根据等腰直角三角形的判定与性质分三种情况:(i)如图2,当PD⊥DE,DP=DE,作PQ⊥x轴;(ii)如图3,当PE⊥DE,PE=DE,作PQ⊥y轴;(iii)如图4,当DP⊥DE,DP=PE,作DM⊥AC,EN⊥AC;进行讨论可求点P的坐标;②动直线l与直线AC的交点为C和动直线l与y轴的交点在x轴下面,并且与前面的直线平行,可求m的取值范围.
,∠DEO=30°,根据等腰直角三角形的判定与性质分三种情况:(i)如图2,当PD⊥DE,DP=DE,作PQ⊥x轴;(ii)如图3,当PE⊥DE,PE=DE,作PQ⊥y轴;(iii)如图4,当DP⊥DE,DP=PE,作DM⊥AC,EN⊥AC;进行讨论可求点P的坐标;②动直线l与直线AC的交点为C和动直线l与y轴的交点在x轴下面,并且与前面的直线平行,可求m的取值范围.
【考点精析】利用二次函数的图象和二次函数的性质对题目进行判断即可得到答案,需要熟知二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将长方形纸片按如图所示的方式折叠,BC、BD为折痕.若∠ABC=25°,则∠DBE的度数为( )
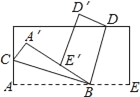
A. 50° B. 65° C. 45° D. 60°
-
科目: 来源: 题型:
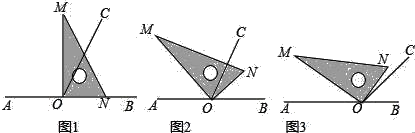
查看答案和解析>>【题目】点O为直线AB上一点,过点O作射线OC,使∠BOC=65°.将一直角三角板的直角顶点放在点O处.
(1)如图①,将三角板MON的一边ON与射线OB重合时,则∠MOC= ;
(2)如图②,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON= ;∠CON= .
(3)将三角板MON绕点O逆时针旋转至图③时,∠NOC=5°,求∠AOM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为线段
为线段 上一动点,分别过点
上一动点,分别过点 作
作 ,
, ,连接
,连接 .已知
.已知 ,设
,设 .
.(1)用含
 的代数式表示
的代数式表示 的值;
的值;(2)探究:当点
 满足什么条件时,
满足什么条件时, 的值最小?最小值是多少?
的值最小?最小值是多少?(3)根据(2)中的结论,请构造图形求代数式
 的最小值.
的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线OM上有三点A、B、C,满足OA=20cm,AB=60cm,BC=10cm,点P从点O出发,沿OM方向以1cm/秒的速度匀速运动,点Q从点C出发在线段CO上向点O匀速运动,两点同时出发,当点Q运动到点O时,点P、Q停止运动.
(1)若点Q运动速度为2cm/秒,经过多长时间P、Q两点相遇?
(2)当P在线段AB上且PA=3PB时,点Q运动到的位置恰好是线段AB的三等分点,求点Q的运动速度;

-
科目: 来源: 题型:
查看答案和解析>>【题目】在每个小正方形的边长为1的网格中,等腰直角三角形ACB与ECD的顶点都在网格点上,点N、M分别为线段AB、DE上的动点,且BN=EM. (Ⅰ)如图①,当BN=
 时,计算CN+CM的值等于
时,计算CN+CM的值等于 
(Ⅱ)当CN+CM取得最小值时,请在如图②所示的网格中,用无刻度的直尺,画出线段CN和CM,并简要说明点M和点N的位置是如何找到的(不要求证明).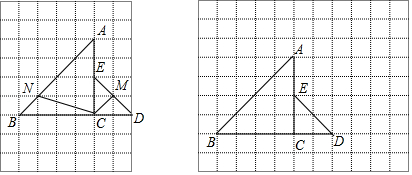
-
科目: 来源: 题型:
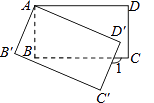
查看答案和解析>>【题目】如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°).若∠1=112°,则∠α的大小是( )
A.68°
B.20°
C.28°
D.22°
相关试题

