【题目】(1)如图1,A(a,0)、B(b,0)且a、b满足|a+4|+![]() =0
=0
①求a、b的值;
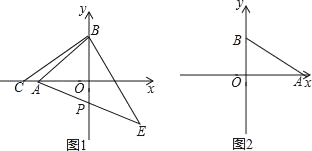
②若C(﹣6,0),连CB,作BE⊥CB,垂足为B,且BC=BE,连AE交y轴于P,求P点坐标;
(2)如图2,若A(6,0),B(0,3),点Q从A出发,以每秒1个单位的速度沿射线AO匀速运动,设点Q运动时间为t秒,过Q点作直线AB的垂线,垂足为D,直线QD与y轴交于E点,在点Q的运动过程中,一定存在△EOQ≌△AOB,请直接写出存在的t值以及相应的E点坐标.
参考答案:
【答案】(1)①a=-4,b=4;②过E点作y轴垂线即可,P(0,-2);(2)两种情况:当t=3时,点E为(0,-6);当t=9时,点E为(0,6).
【解析】
试题(1)本题考查三角形全等的判定,根据题目中的信息求出相应的点的坐标,可以根据题目中的信息画出相应的图形,关键是正确分析题目中的信息,求出所要求的结论.①由a、b满足![]() ,可以求得a、b的值.②作EF⊥y轴于点F,根据题目中的信息,可以推出△BCO≌△EBF,然后根据对应关系求出对应边的长度,从而可以求得点P的坐标.(2)根据题意可以画出相应的图象,从而可以直接写出t的值和相应的点E的值.
,可以求得a、b的值.②作EF⊥y轴于点F,根据题目中的信息,可以推出△BCO≌△EBF,然后根据对应关系求出对应边的长度,从而可以求得点P的坐标.(2)根据题意可以画出相应的图象,从而可以直接写出t的值和相应的点E的值.
试题解析:(1)①∵a、b满足|a+4|+![]() =0, ∴a+4=0,a+b=0. 解得,a=-4,b=4.
=0, ∴a+4=0,a+b=0. 解得,a=-4,b=4.
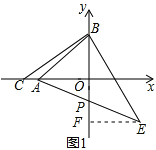
②如图所示:作EF⊥y轴于点F, 则∠EFB=90°. ∵BE⊥CB,垂足为B,且BC=BE,∠BOC=90°,
∴∠COB=∠EFB,∠CBO=∠BEF. ∴△BCO≌△EBF. ∵A(-4,0)B(4,0),C(-6,0),
∴EF=OB=4,BF=OC=6. ∴点E的坐标为(4,-2). ∵A(-4,0).
设过点A、E的解析式为:y=kx+b.
则![]() . 解得,k=
. 解得,k=![]() ,b=1. ∴y=
,b=1. ∴y=![]() x1.
x1.
令x=0,则y=-1. 故点P的坐标为(0,-1).
(2)根据题意,分两种情况:
第一种情况如图所示:
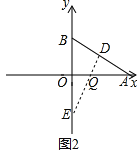
∵A(6,0),B(0,3),△EOQ≌△AOB, ∴OQ=OB,OE=OA.
∴AQ=3,点E的坐标为(0,-6). ∵点Q从A出发,以每秒1个单位的速度沿射线AO匀速运动,
∴点Q运动的时间t=3秒. 故此时t的值为3,点E的坐标为(0,-6).
第二种情况如下图所示:
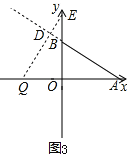
∵A(6,0),B(0,3),△EOQ≌△AOB, ∴OQ=OB,OE=OA.
∴AQ=9,点E的坐标为(0,6). ∵点Q从A出发,以每秒1个单位的速度沿射线AO匀速运动,
∴点Q运动的时间t=9秒. 故此时t的值为9,点E的坐标为(0,6).
-
科目: 来源: 题型:
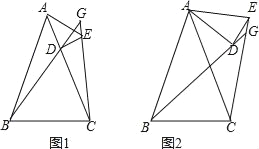
查看答案和解析>>【题目】已知AB=AC,AD=AE,∠BAC=∠DAE,直线BD、CE交于点G,
(1)如图1,点D在AC上,求证:∠BGC=∠BAC;
(2)如图2,当点D不在AC上,(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由.
-
科目: 来源: 题型:
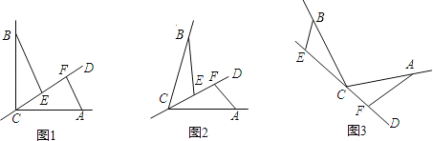
查看答案和解析>>【题目】CD经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图1,若∠BCA=90°,∠α=90°,则BE_____CF;EF_____|BE﹣AF|(填“>”,“<”或“=”);
②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件_____,使①中的两个结论仍然成立。
(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想并给出理由。.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在方格纸中(小正方形的边长为1),△ABC的三个顶点均为格点,将△ABC沿x轴向左平移5个单位长度,根据所给的直角坐标系(O是坐标原点),解答下列问题:

(1)画出平移后的△A′B′C′,并直接写出点A′、B′、C′的坐标;
(2)求出在整个平移过程中,△ABC扫过的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式,能够表示图中阴影部分的面积的是( )
①ac+(b﹣c)c;②ac+bc﹣c2;③ab﹣(a﹣c)(b﹣c);④(a﹣c)c+(b﹣c)c+c2

A. ①②③④ B. ①②③ C. ①② D. ①
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1=65°,∠2=50°,∠3=115°,EG平分∠NEF,
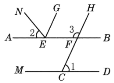
试说明:(1)AB∥CD;
(2)EG∥FH的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是中国古代数学专著,在数学上有其独到的成就,不仅最早提到了分数问题,也首先记录了“盈不足”等问题.如有一道阐述“盈不足”的问题,原文如下:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?译文为:现有若干人合伙出钱买鸡,如果每人出9文钱,就会多11文钱;如果每人出6文钱,又会缺16文钱.问买鸡的人数、鸡的价格各是多少?请解答上述问题.
相关试题

