【题目】问题发现:如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE
(1)填空:①∠AEB的度数为;②线段BE、AD之间的数量关系是 .
(2)拓展探究:如图2,△ACB和△DCE均为等腰三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.
参考答案:
【答案】
(1)60°;AD=BE
(2)
①∵△ACB与△DCE都为等腰直角三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=90°,∠CDE=∠CED=45°,
∴∠ADC=180°﹣∠CDE=135°,
∵∠ACD+∠DCB=∠ECB+∠DCB=90°
∴∠ACD=∠ECB,
∴在△ACD与△BCE中有

∴△ACD≌△BCE(SAS),
∴∠BEC=∠ADC=135°,AD=BE,
∴∠AEB=∠BEC﹣∠CED=90°,
故∠AEB的度数为90°;
②∵CM⊥DE,△CDE为等腰直角三角形,
∴DM=DE(三线合一)
∴CM= ![]() DE,
DE,
∴AE=AD+DE=BE+2CM,
即:线段CM、AE、BE之间的数量关系为:AE=BE+2CM
【解析】解:(1)∵△ACB与△DCE都为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°,∠CDE=∠CED=60°,
∴∠ADC=180°﹣∠CDE=60°,
∵∠ACD+∠DCB=∠ECB+∠DCB=60°
∴∠ACD=∠ECB,
∴在△ACD与△BCE中有
∴△ACD≌△BCE(SAS),
∴∠BEC=∠ADC=120°,AD=BE,
∴∠AEB=∠BEC﹣∠CED=60°,
故答案为:60°,AD=BE;
(1)根据已知条件可以判定:△ACD≌△BCE,可得AD=BE,再由角度关系求得∠AEB=60°;(2)同(1)可证:△ACD≌△BCE,得到AD=BE,∠AEB=90°,再由CM⊥DE,可得CM= ![]() DE,进而可求得线段CM、AE、BE之间的数量关系为:AE=BE+2CM.
DE,进而可求得线段CM、AE、BE之间的数量关系为:AE=BE+2CM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,最适合采用普查方式的是( )
A.奥运会上对参赛运动员进行尿样检查
B.调查市面上一次性筷子的卫生情况
C.对电视剧“蓝色大海的传说”收视率的调查
D.调查重庆市初三年级学生每天所完成家庭作业的时间
-
科目: 来源: 题型:
查看答案和解析>>【题目】(4a2b﹣5ab2)﹣(3a2b﹣4ab2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算﹣2+1的结果是( )
A.-3
B.-1
C.3
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】父亲告诉小明:“距离地面越高,温度越低,”并给小明出示了下面的表格。
距离地面高度(千米)
0
1
2
3
4
5
温度(℃)
20
14
8
2
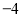
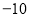
根据上表,父亲还给小明出了下面几个问题,你和小明一起回答。
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用h表示距离地面的高度,用t表示温度,那么随着h的变化,t是怎么变化的?
(3)你能猜出距离地面6千米的高空温度是多少吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】实验初中组织了“英语手抄报”征集活动,现从中随机抽取部分作品,按A、B、C、D四个等级进行评价,并根据统计结果绘制了如下两幅不完整的统计图.

(1)抽取了_____份作品;
(2)此次抽取的作品中等级为B的作品有______份,并补全条形统计图;
(3)若该校共征集到600份作品,请估计等级为A的作品约有多少份?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若n边形的内角和是它的外角和的2倍,则n= .
相关试题

