【题目】如图,直线l上依次有三点A、B、C,且AB=8、BC=16,点P为射线AB上一动点,将线段AP进行翻折得到线段PA’(点A落在直线l上点A’处、线段AP上的所有点与线段PA’上的点对应)如图1

(1)若翻折后A’C=2,则翻折前线段AP= ;
(2)若点P在线段BC上运动,点M为线段A’C的中点,求线段PM的长度;
(3)若点P 在线段BC上运动,点N为B’P的中点,点M为线段A’C的中点,设AP=x,用x表示A’M+PN.
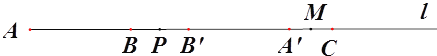
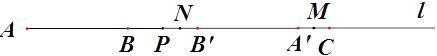
参考答案:
【答案】(1) 11 ;(2) PM=12 ;(3)  .
.
【解析】试题分析:
(1)如图1,由题意可知:AA′=AB+BC-A′C=22,由AP=A′P可得AP=11;
(2)如图3当点A′在点C的左侧时,由(1)可得此时AA′=22,结合已知易得此时:PM=PA′+A′M= ![]() =
= ![]() =
=![]() =12;如图4,当点A′在点C的右侧时,同理可得:PM=PA′-A′M=
=12;如图4,当点A′在点C的右侧时,同理可得:PM=PA′-A′M= ![]() =
=![]() =
= ![]() =12 ;由此即可得到PM=12;
=12 ;由此即可得到PM=12;
(3)根据题意分:①当8<x<12;②当x>12两种情况结合图5、图6分析解答即可.
试题解析:
(1)如图1,当翻折后点A′在点C的左侧时,∵AB=8,BC=16,A′C=2,
∴AA′=AB+BC-A′C=22,
又∵由折叠的性质可知:AP=A′P,
∴AP=11;

(2)①当A′在点C的左侧时,如图3,

由题知PA=PA′,
∵M为AC中点,
∴MA′=MC,
∴PM=PA′+A′M= ![]() =
= ![]() =
=![]() =12;
=12;
②当A′在点C的右侧时,如图4,

∵M为A′C中点,
∴MA′=MC,
∴PM=PA′-A′M= ![]() =
=![]() =
= ![]() =12 ;
=12 ;
综上可得:PM=12 ;
(3)①当8<x<12 此时,A′在C的左侧,如图5,

PB′=PB=x-8,
∵N为BP中点,
∴![]() ,
,
∵A′C=24-2x,
∵M为A′C中点,
∴![]() ,
,
∴![]()
![]() ;
;
②当x>12 ,此时,A′在C的右侧,如图6

PB′=PB=x-8, ![]() ,
,
A′C=2x-24,
∵M为A′C中点,
∴![]() ,
,
∴![]()
![]() ;
;
③当x>24时,如图7,点P不在线段BC上了,不予考虑,
![]()
∴综上所述:  .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
(1)求证:BC是⊙O的切线;
(2)连接AF,BF,求∠ABF的度数;
(3)如果CD=15,BE=10,sinA=
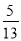 ,求⊙O的半径.
,求⊙O的半径.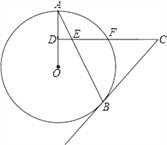
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=2(x﹣3)2+4顶点坐标是( )
A.(3,4)
B.(﹣3,4)
C.(3,﹣4)
D.(2,4) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上点A、B所表示的数分别是4,8,
(1)请用尺规作图的方法确定原点O的位置(不写做法,保留作图痕迹)
(2)已知动点M从点A出发,以每秒1个单位长度的速度沿数轴向左匀速运动,同时点N从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.
①运动1秒后,点M表示的数是_____,点N表示的数为______
②运动t秒后,点M表示的数是_____,点N表示的数为______
③若线段BN=2,求此时t的大小以及相应的M所表示的数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从下列不等式中选择一个与x+1≥2组成不等式组,若要使该不等式组的解集为x≥1,则可以选择的不等式是( )
A. x>0 B. x>2 C. x<0 D. x<2
-
科目: 来源: 题型:
查看答案和解析>>【题目】安徽省2010年末森林面积为3804.2千公顷,用科学记数法表示3804.2千正确的是( )
A.3804.2×103B.380.42×104C.3.8042×106D.3.8042×105
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)在图1中,画一个三角形,使它的三边长都是有理数;
(2)在图2中,画一个直角三角形,使它们的三边长都是无理数;
(3)在图3中,画一个正方形,使它的面积是10.
相关试题

