【题目】如图![]() 、
、![]() ,在平行四边形
,在平行四边形![]() 中,
中,![]() 、
、![]() 的角平分线
的角平分线![]() 、
、![]() 分别与线段
分别与线段![]() 两侧的延长线(或线段
两侧的延长线(或线段![]() )相交与
)相交与![]() 、
、![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .
.
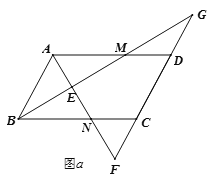
(1)在图![]() 中,求证:
中,求证:![]() ,
,![]() .
.
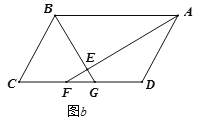
(2)在图![]() 中,仍有(1)中的
中,仍有(1)中的![]() ,
,![]() 成立,请解答下面问题:
成立,请解答下面问题:
①若![]() ,
,![]() ,
,![]() ,求
,求![]() 和
和![]() 的长;
的长;
②是否能给平行四边形![]() 的边和角各添加一个条件,使得点
的边和角各添加一个条件,使得点![]() 恰好落在
恰好落在![]() 边上且
边上且![]() 为等腰三角形?若能,请写出所给条件;若不能,请说明理由.
为等腰三角形?若能,请写出所给条件;若不能,请说明理由.
参考答案:
【答案】(1)见解析;(2)①![]() ,
,![]() ,②
,②![]() ,
,![]() ,见解析.
,见解析.
【解析】
(1)由平行线的性质和角平分线的性质即可证明结论;
(2)①由(1)题的思路可求得FG的长,再证明△BCG是等边三角形,从而得![]() ,过点
,过点![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]() ,在Rt△AFH中用勾股定理即可求出AF的长;
,在Rt△AFH中用勾股定理即可求出AF的长;
②若使点![]() 恰好落在
恰好落在![]() 边上且
边上且![]() 为等腰三角形,易得F、G两点重合于点E,再结合(1)(2)的结论进行分析即可得到结论.
为等腰三角形,易得F、G两点重合于点E,再结合(1)(2)的结论进行分析即可得到结论.
解:(1)∵四边形![]() 是平行四边形,∴
是平行四边形,∴![]() ,
,![]() .
.
∴![]() ,
,
又∵![]() 、
、![]() 是
是![]() 与
与![]() 的角平分线,
的角平分线,
∴![]() ,即∠AEB=90°,
,即∠AEB=90°,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
又∵![]() 是
是![]() 的角平分线、
的角平分线、
∴![]() ,
,
∴![]() .
.
同理可得![]() .
.
∴![]() ;
;
(2)解:①由已知可得,![]() 、
、![]() 仍是
仍是![]() 与
与![]() 的角平分线且
的角平分线且![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() .
.
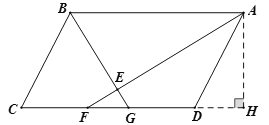
如图,过点![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]() .
.
∵![]() ,
,![]() ,
,![]() .
.
![]() .
.
∵![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() .
.
②![]() ,
,![]() (类似答案均可).
(类似答案均可).
若使点![]() 恰好落在
恰好落在![]() 边上,则易得F、G两点重合于点E,又由(1)(2)的结论知
边上,则易得F、G两点重合于点E,又由(1)(2)的结论知![]() ,
,![]() ,所以平行四边形的边应满足
,所以平行四边形的边应满足![]() ;
;
若使点![]() 恰好落在
恰好落在![]() 边上且
边上且![]() 为等腰三角形,则EA=EB,所以∠EAB=∠EBA,
为等腰三角形,则EA=EB,所以∠EAB=∠EBA,
又因为![]() 、
、![]() 仍是
仍是![]() 与
与![]() 的角平分线,所以∠CBA=∠BAD=90°,所以∠C=90°.
的角平分线,所以∠CBA=∠BAD=90°,所以∠C=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用小立方块搭一个几何体,使它从正面、上面看到的形状图如图所示,从上面看到的形状图的小正方形中的字母表示在该位置小立方块的个数.试回答下列问题:

(1)a,b,c各表示几?
(2)这个几何体最少有几个小立方块搭成?最多呢?
(3)当d=e=1,f=2时,画出这个几何体从左面看到的形状图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“四书五经”是中国的“圣经”,“四书五经”是《大学》、《中庸》、《论语》和《孟子》(四书)及《诗经》、《尚书》、《易经》、《礼记》、《春秋》(五经)的总称,这是一部被中国人读了几千年的教科书,包含了中国古代的政治理想和治国之道,是我们了解中国古代社会的一把钥匙,学校计划分阶段引导学生读这些书,计划先购买《论语》和《孟子》供学生使用,已知用500元购买《孟子》的数量和用800元购买《论语》的数量相同,《孟子》的单价比《论语》的单价少15元.
(1)求《论语》和《孟子》这两种书的单价各是多少?
(2)学校准备一次性购买这两种书
 本,但总费用不超过
本,但总费用不超过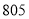 元,那么这所学校最多购买多少本《论语》?
元,那么这所学校最多购买多少本《论语》? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,不透明圆锥体DEC放在直线BP所在的水平面上,且BP过圆锥底面圆的圆心,圆锥的高为2
 m,底面半径为2 m,某光源位于点A处,照射圆锥体在水平面上留下的影长BE=4 m.
m,底面半径为2 m,某光源位于点A处,照射圆锥体在水平面上留下的影长BE=4 m.(1)求∠ABC的度数;
(2)若∠ACP=2∠ABC,求光源A距水平面的高度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,OA平分∠EOC.

(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价8.5折优惠.设顾客预计累计购物
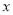 元(
元(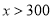 ).
).(1)请用含
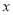 的代数式分别表示顾客在两家超市购物所付的费用;
的代数式分别表示顾客在两家超市购物所付的费用;(2)李明准备购买500元的商品,你认为他应该去哪家超市?请说明理由;
(3)计算一下,李明购买多少元的商品时,到两家超市购物所付的费用一样?
-
科目: 来源: 题型:
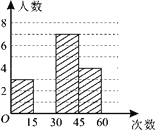
查看答案和解析>>【题目】在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
(1)频数分布表中a = ,b= ,并将统计图补充完整;
(2)如果该校七年级共有女生180人,估计仰卧起坐能够一分钟完成30或30次以上的女学生有多少人?
(3)已知第一组中只有一个甲班学生,第四组中只有一个乙班学生,老师随机从这两个组中各选一名学生谈心得体会,则所选两人正好都是甲班学生的概率是多少?

相关试题

