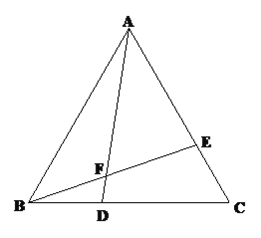
【题目】已知:如图,△ABC是等边三角形,点D、E分别在边BC、AC上,且BD=CE,AD与BE相交于点F.
(1)求证:△ABD≌△BCE
(2)求证: ![]()
参考答案:
【答案】(1)证明见解析;(2)证明见解析
【解析】试题分析:
(1) 要证△ABD≌△BCE,利用△ABC是等边三角形可以得到,AB=BC,∠ABC=∠BCA. 在这种情况下观察图形可知,在待证明的两个三角形中已经获得一组对应边相等和一组对应角相等,再根据已知条件BD=CE,根据SAS即可证明这两个三角形全等.
(2) 观察待证明的等式形式可知,AE应为BE和EF的比例中项. 将待证明的等式改写为比例式后,利用“三点定形法”可以找到一组合适的相似三角形△EBA与△EAF. 观察这两个三角形发现:这两个三角形有一组对应角为公共角;对于另一组对应角∠EBA与∠EAF而言,可以通过第(1)问中的全等三角形和△ABC的性质证明其相等. 利用相似三角形的判定定理即可获得这组三角形相似,进而证明等式成立.
试题解析:
(1) ∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠BCA,即∠ABD=∠BCE,
∵在△ABD与△BCE中:
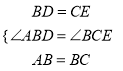 ,
,
∴△ABD≌△BCE (SAS).
(2) ∵△ABC是等边三角形,
∴∠ABC=∠BAC,
∵△ABD≌△BCE,
∴∠BAD=∠CBE,
∴∠ABC-∠CBE =∠BAC-∠BAD,
∴∠EBA=∠CAD,即∠EBA=∠EAF,
∵在△EBA与△EAF中:
∠AEB=∠FEA (公共角),∠EBA=∠EAF,
∴△EBA∽△EAF,
∴![]() ,
,
即AE2=BE·EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)观察下列各式:
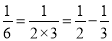 ,
,  ,
, 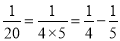 ,
, 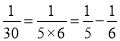 ,……,由此可推断
,……,由此可推断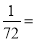 = .
= .(2)请猜想能表示(1)的特点的一般规律,用含
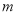 的等式表示出来为 = .(
的等式表示出来为 = .( 表示正整数)
表示正整数) (3)请参考(2)中的规律计算:
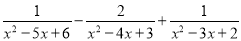
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解方程

(2)先化简,再求值
 其中
其中
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果飞机离地面6000米记为+6000米,现在它又下降了1600米,那么现在飞机的高度可记为米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:
(1)3a2-27b2; (2)x2-8(x-2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】班主任要从甲、乙两名跳远运动员中挑选一人参加校运动会比赛.在最近的10次选拔赛中,他们的成绩如下(单位:cm):
甲
585
596
610
598
612
597
604
600
613
601
乙
613
618
580
574
618
593
585
590
598
624
(1)他们的平均成绩分别是多少?
(2)甲、乙两名运动员这10次比赛成绩的极差、方差分别是多少?
(3)怎样评价这两名运动员的运动成绩?
(4)历届比赛表明,成绩达到5.96m就有可能夺冠,你认为为了夺冠应选择谁参加这项比赛?如果历届比赛成绩表明,成绩达到6.10m就能打破记录,那么你认为为了打破记录应选择谁参加这项比赛?
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:x2+x= .
相关试题

