Question

【题目】如图，在△ABC中，AB=AC，∠BAC=90，BD是的平分线，CE⊥BD，垂足是E，BA和CE的延长线交于点F．

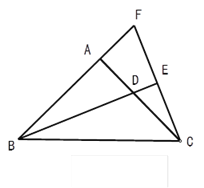
（1）在图中找出与△ABD全等的三角形，并说出全等的理由；

（2）说明BD=2EC；

（3）如果AB=5，BC=5求AD的长．

Answer 1

【答案】（1）理由见解析；(2)理由见解析；(3) 55.

【解析】分析（1）可利用ASA判断△ABD≌△ACF；（2）根据（1）可得BD=CF，证明△BFE≌△BCE，可得出EF=CE=CF，继而可得出结论；（3）过D作DM⊥BC，设AD=DM=MC=x，则可得DC=x，根据AD+DC=AC=AB=5，可得关于x的方程，解出即可得出答案．

本题解析：

证明：(1)△ABD≌△ACF.

∵AB=AC,∠BAC=90，

∴∠FAC=∠BAC=90，

∵BD⊥CE,∠BAC=90，

∴∠ADB=∠EDC，

∴∠ABD=∠ACF，

∵在△ABD和△ACF中，

，

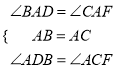∴△ABD≌△ACF(ASA)，

(2)∵△ABD≌△ACF，

∴BD=CF，

∵BD⊥CE，

∴∠BEF=∠BEC，

∵BD是∠ABC的平分线，

∴∠FBE=∠CBE，

∵在△FBE和△CBE中，

，

∴△FBE≌△CBE(ASA)，

∴EF=EC，

∴CF=2CE，

∴BD=2CE.

(3)过D作DM⊥BC，

∵AB=BM,设AD=DM=MC=x，

则 BC=MB+MC即5=5+x

解得：x=55，

则AD的长为55.