【题目】△ADE中,AE=AD,∠EAD=90°.


(1)如图(1),若EC、DB分别平分∠AED、∠ADE,交AD、AE于点C、B,连接BC.请你判断AB、AC是否相等,并说明理由;
(2)△ADE的位置保持不变,将(1)中的△ABC绕点A逆时针旋转至图
(2)的位置,CD、BE相交于O,请你判断线段BE与CD的位置关系及数量关系,并说明理由;
(3)在(2)的条件下,若CD=6,试求四边形CEDB的面积.
参考答案:
【答案】(1)理由见解析;(2)理由见解析;(3)18.
【解析】分析:(1)由已知得∠AEC=∠ADB,AE=AD,∠A=∠A,利用“ASA”证明△AEC≌△ADB即可;(2)BE=CD且BE⊥CD.由旋转的性质可证△AEB≌△ADC,从而可得BE=CD,再利用角的相等关系,互余关系证明BE⊥CD;(3)由于BE⊥CD,BE=CD=6,当四边形的对角线互相垂直时,四边形的面积等于对角线积的一半.
本题解析:
(1)AB=AC.
理由如下:
∵EC、DB分别平分∠AED、∠ADE
∴∠AEC=![]() ∠AED,∠ADB=
∠AED,∠ADB=![]() ∠ADE
∠ADE
∵∠AED=∠ADE
∴∠AEC=∠ADB
在△AEC和△ADB中,
∠AEC=∠ADB,AE=AD,∠A=∠A
∴△AEC≌△ADB
∴AB=AC;
(2)BE=CD且BE⊥CD.
理由如下:
∵∠EAD=∠BAC
∴∠EAB=∠DAC
在△AEB和△ADC中,
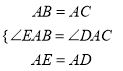 ,
,
∴△AEB≌△ADC(SAS)
∴EB=CD
∴∠AEB=∠ADC
∵∠AEB+∠DEB+∠ADE=90°
∴∠ADC+∠DEB+∠ADE=90°
∵∠ADC+∠DEB+∠ADE+∠DOE=180°
∴∠DOE=90°
∴BE⊥CD;
(3)四边形CEDB的面积=![]() ×BE×CD=
×BE×CD=![]()
![]() =18.
=18.
-
科目: 来源: 题型:
查看答案和解析>>【题目】圆是( )图形.
A.中心对称
B.轴对称
C.中心对称和轴对称
D.以上都不对 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的每个内角均为150°,则这个多边形是( )
A.八边形B.九边形C.十边形D.十二边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】不在同一条直线上的三个点可以确定( )个圆.
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点M(﹣1,3),先向右平移2个单位,再向下平移4个单位,得到的点的坐标为( )
A.(﹣3,﹣1)B.(﹣3,7)C.(1,﹣1)D.(1,7)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016广东省梅州市第15题)如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(
 ,0),B(0,2),则点B2016的坐标[来为______________.
,0),B(0,2),则点B2016的坐标[来为______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=90,BD是
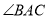 的平分线,CE⊥BD,垂足是E,BA和CE的延长线交于点F.
的平分线,CE⊥BD,垂足是E,BA和CE的延长线交于点F.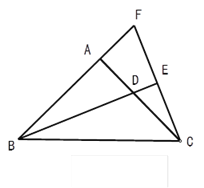
(1)在图中找出与△ABD全等的三角形,并说出全等的理由;
(2)说明BD=2EC;
(3)如果AB=5,BC=5
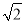 求AD的长.
求AD的长.
相关试题

