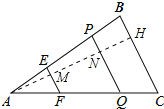
【题目】如图,△ABC中,点E、P在边AB上,且AE=BP,过点E、P作BC的平行线,分别交AC于点F、Q,记△AEF的面积为S1,四边形EFQP的面积为S2,四边形PQCB的面积为S3.

(1)求证:EF+PQ=BC;
(2)若S1+S3=S2,求![]() 的值;
的值;
(3)若S3﹣S1=S2,直接写出![]() 的值.
的值.
参考答案:
【答案】(1)见解析;(2)2;(3)![]() .
.
【解析】
试题分析:(1)由平行线得出比例式![]() ,
,![]() ,证出AP=BE,得出
,证出AP=BE,得出![]() =1,即可得出EF+PQ=BC;
=1,即可得出EF+PQ=BC;
(2)过点A作AH⊥BC于H,分别交PQ于M、N,设EF=a,PQ=b,AM=h,则BC=a+b,由平行线得出△AEF∽△APQ,得出![]() =
=![]() ,得出AN=
,得出AN=![]() ,MN=(
,MN=(![]() ﹣1)h,
﹣1)h,
由三角形的面积公式得出S1=![]() ah,S2=
ah,S2=![]() (a+b)(
(a+b)(![]() ﹣1)h,S3=
﹣1)h,S3=![]() (b+a+b)h,得出
(b+a+b)h,得出![]() ah+
ah+![]() (a+b+b)h=
(a+b+b)h=![]() (a+b)(
(a+b)(![]() ﹣1)h,求出b=3a,即可得出结果;(3)由题意得出
﹣1)h,求出b=3a,即可得出结果;(3)由题意得出![]() (a+b+b)h﹣
(a+b+b)h﹣![]() ah=
ah=![]() (a+b)(
(a+b)(![]() ﹣1)h,得出b=(1+
﹣1)h,得出b=(1+![]() )a,即可得出结果.
)a,即可得出结果.
(1)证明:∵EF∥BC,PQ∥BC,
∴![]() ,
,![]() ,
,
∵AE=BP,
∴AP=BE,
∴![]() =
=![]() =1,
=1,
∴![]() =1,
=1,
∴EF+PQ=BC;
(2)解:过点A作AH⊥BC于H,分别交PQ于M、N,如图所示:
设EF=a,PQ=b,AM=h,
则BC=a+b,
∵EF∥PQ,
∴△AEF∽△APQ,
∴![]() =
=![]() ,
,
∴AN=![]() ,MN=(
,MN=(![]() ﹣1)h,
﹣1)h,
∴S1=![]() ah,S2=
ah,S2=![]() (a+b)(
(a+b)(![]() ﹣1)h,S3=
﹣1)h,S3=![]() (b+a+b)h,
(b+a+b)h,
∵S1+S3=S2,
∴![]() ah+
ah+![]() (a+b+b)h=
(a+b+b)h=![]() (a+b)(
(a+b)(![]() ﹣1)h,
﹣1)h,
解得:b=3a,
∴![]() =3,
=3,
∴![]() =2;
=2;
(3)解:∵S3﹣S1=S2,
∴![]() (a+b+b)h﹣
(a+b+b)h﹣![]() ah=
ah=![]() (a+b)(
(a+b)(![]() ﹣1)h,
﹣1)h,
解得:b=(1±![]() )a(负值舍去),
)a(负值舍去),
∴b=(1+![]() )a,
)a,
∴![]() =1+
=1+![]() ,
,
∴![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程(1﹣m2)x2+2(1﹣m)x﹣1=0有两个实数根,求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,属于定义的是( )
A. 两点确定一条直线 B. 同角或等角的余角相等
C. 两直线平行,内错角相等 D. 点到直线的距离是该点到这条直线的垂线段的长度
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形一定是相似图形的是( )
A.任意两个菱形
B.任意两个正三角形
C.两个等腰三角形
D.两个矩形 -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场统计了每个营业员在某月的销售额,统计图如下,根据统计图中给出的信息,解答下列问题:
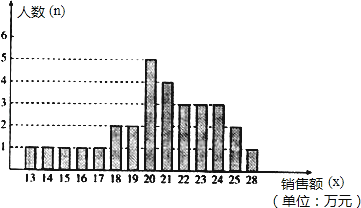
(1)设营业员的月销售额为x(单位:万元),商场规定:当x<15时为不称职,当15≤x<20时,为基本称职,当20≤x<25为称职,当x≥25时为优秀.称职和优秀的营业员共有多少人?所占百分比是多少?
(2)根据(1)中规定,所有称职以上(职称和优秀)的营业员月销售额的中位数、众数和平均数分别是多少?
(3)为了调动营业员的工作积极性,决定制定月销售额奖励标准,凡到达或超过这个标准的营业员将受到奖励.如果要使得称职以上(称职和优秀)的营业员有一半能获奖,你认为这个奖励标准应定月销售额为多少元合适?并简述其理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BF=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )
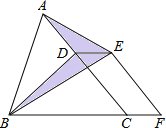
A.3 B.4 C.6 D.8
-
科目: 来源: 题型:
查看答案和解析>>【题目】超市有一种“喜之郎”果冻礼盒,内装两个上下倒置的果冻,果冻高为4cm,底面是个直径为6cm的圆,横截面可以近似地看作一个抛物线,为了节省成本,包装应尽可能的小,那么要制作这样一个包装盒至少纸板( )平方厘米.(不计重合部分)
A.253 B.288 C.206 D.245
相关试题

