【题目】如图，已知二次函数y=a（x﹣h）2+的图象经过原点O（0，0），A（2，0）．

写出该函数图象的对称轴；

参考答案：

【答案】对称轴为直线x=1

【解析】试题分析：

本题要求二次函数的对称轴. 分析题目条件可知本题可以用两种方法解决. 其一，因为已知的两个点均为二次函数与x轴的交点，所以点O与点A必定关于二次函数的对称轴对称. 根据对称性可知，该二次函数的对称轴与x轴的交点必定是线段OA的中点. 利用该几何性质容易得到该二次函数的对称轴. 其二，由于点O与点A均在二次函数的图象上，所以点O与点A的坐标一定满足该二次函数的解析式. 将这两点的坐标代入解析式并联立，即可得到一个方程组，解之可得a与h的值. 这样就确定了该二次函数的解析式，进而可以获得二次函数的对称轴.

试题解析：

(解法一)

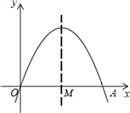
如图，设该二次函数的对称轴与x轴的交点为M.

∵点O与点A均为该二次函数与x轴的交点，

∴点O与点A关于该二次函数的对称轴对称，

∴在x轴上，线段OA的中点为点M，即，

∵点O的坐标为(0, 0)，点A的坐标为(2, 0)，

∴OA=2，

∴，

∴点M的坐标为(1, 0)，

∵点M为该二次函数的对称轴与x轴的交点，

∴该二次函数的对称轴为直线x=1.

(解法二)

∵二次函数的图象经过点O(0, 0)与点A(2, 0)，

∴将点O与点A的坐标代入二次函数解析式，得

，

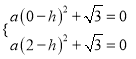解这个方程组：

，

∵，

∴，即,①

∵在二次函数中，a≠0，

∴①式两侧同时除以a，得 h=1.

∴.

∴该二次函数的解析式为.

∴该二次函数的对称轴为直线x=1.

关闭