【题目】好学的小宸利用电脑作了如下的探索:
(1)如图①,将边长为2的等边三角形复制若干个后向右平移,使一条边在同一直线上.则△A2C1B1的面积为 ;
(2)求△A4C3B3的面积;
(3)在保持图①中各三角形的边OB1=B1B2=B2B3=B3B4=2不变的前提下,小宸又作了如下探究:将顶点A1、A2、A3、A4向上平移至同一高度(如图②),若OA4=OB4,试判断以OA2、OA3和OA4为三边能否构成三角形?若能,请判断这个三角形的形状;若不能,请说明理由.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .(3)这三边能构成直角三角形.
.(3)这三边能构成直角三角形.
【解析】
试题分析:(1)分别过A2、C1作x轴的垂线,垂足分别为E、F,根据勾股定理求得相应线段的长度,由△A2C1B1=S梯形A1EFC1-△C1FB1-△A2EB1可求得;
(2)分别计算△A4B3B4、△A4OB4的面积,利用相似三角形即可求出△A4C3B3的面积;
(3)根据勾股定理的逆定理即可判定三角形为直角三角形.
试题解析:(1) ![]() ;
;
(2)解得△A4B3B4的面积为:![]()
解得△A4OB4的面积为:![]()
利用△OC3B3∽△OA4B4得:S四边形C3B3B4A4:S△OA4B4=7:16
∴四边形C3B3B4A4的面积为:![]()
∴△A4C3B3的面积为:![]() .
.
(3)能.
设这些等腰三角形的高为h.
则:OA22=9+h2,
OA32=25+h2,
OA42=64
∵OA4=OB4
∴∠OA4B=∠OB4A4=∠A4B3B4
∴△OA4B4∽△A4B4B3
∴![]()
∴A4B4=4
∴h2=15
∴OA22+OA32=OA42
即这三边能构成直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:2a2+ab= .
-
科目: 来源: 题型:
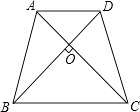
查看答案和解析>>【题目】如图,欲用一块面积为800cm2的等腰梯形彩纸作风筝,用竹条作梯形的对角线且对角线恰好互相垂直,那么需要竹条多少厘米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. a2+a2=a4B. a3÷a=a3C. a2a3=a5D. (a2)4=a6
-
科目: 来源: 题型:
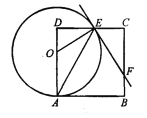
查看答案和解析>>【题目】如图,点O在边长为8的正方形ABCD的AD边上运动(4<C)A<8),以O为圆心,OA长为半径作圆,交CD于点E,连接OE、AE,过点E作直线EF交BC于 点F,且∠CEF=2∠DAE.
(1)求证:直线EF为⊙O的切线;
(2)在点O的运动过程中,设DE=x,解决下列问题:
①求OD·CF的最大值,并求此时半径的长;
②试猜想并证明△CEF的周长为定值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在凸多边形中, 四边形有2条对角线, 五边形有5条对角线, 经过观察、探索、归纳, 你认为凸八边形的对角线条数应该是多少条? 简单扼要地写出你的思考过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x-2=2-x的解是______.
相关试题

