【题目】已知:如图,AB是⊙O的直径,BC是弦,∠B=30°,延长BA到D,使∠BDC=30°.
(1)求证:DC是⊙O的切线;
(2)若AB=2,求DC的长.
参考答案:
【答案】
(1)解:连接OC.
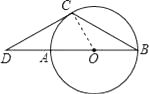
∵OB=OC,∠B=30°,
∴∠OCB=∠B=30°,
∴∠COD=∠B+∠OCB=60°,
∵∠BDC=30°,
∴∠BDC+∠COD=90°,DC⊥OC,
∵BC是弦,
∴点C在⊙O上,
∴DC是⊙O的切线,点C是⊙O的切点;
(2)解:∵AB=2,
∴OC=OB= ![]() =1,
=1,
∵在Rt△COD中,∠OCD=90°,∠D=30°,
∴DC= ![]() OC=
OC= ![]() .
.
【解析】(1)连接OC,根据已知易证明∠COD=60°,再利用三角形内角和定理求出∠DCO的度数,即可证得DC⊥OC,根据切线的判定定理即可证得结论。
(2)根据已知求出OC的长,然后在Rt△COD中,利用解直角三角形求出DC的长即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△AOB中,∠AOB=90°,∠BAO=30°,以AB为一边作等边△ABE,作OA的垂直平分线MN交AB的垂线AD于点D.
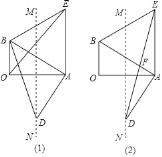
(1)连接BD,OE.求证:BD=OE;
(2)连接DE交AB于F.求证:F为DE的中点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果a c b ,那么我们规定(a,b)=c,例如:因为23 8 ,所以(2,8)=3.
(1)根据上述规定,填空:(3,27)= ,(4,1)= ,(2,
 )= ;
)= ;(2)若记(3,5)=a,(3,6)=b,(3,30)=c,求证: a b c .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个口袋中有4个完全相同的小球,把它们分别标号为1、2、3、4,随机摸取一个小球然后放回,再随机地摸取一个小球.
(1)采用树状图法(或列表法)列出两次摸取小球出现的所有可能结果,并回答摸取两球出现的所以可能结果共有几种;
(2)求两次摸取的小球标号相同的概率;
(3)求两次摸取的小球标号的和等于4的概率;
(4)求两次摸取的小球标号的和是2的倍数或3的倍数的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=6,AC=4,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC分别交AB、AC于M、N,则△AMN的周长为( )
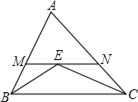
A. 12B. 10C. 8D. 不确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】[知识生成]通常,用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.
例如:如图①是一个长为
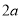 ,宽为
,宽为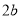 的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.请解答下列问题:
的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.请解答下列问题: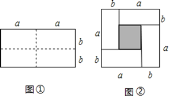
(1)图②中阴影部分的正方形的边长是________________;
(2)请用两种不同的方法求图②中阴影部分的面积:
方法1:________________________;方法2:_______________________;
(3)观察图②,请你写出(a+b)2、
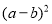 、
、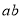 之间的等量关系是____________________________________________;
之间的等量关系是____________________________________________;(4)根据(3)中的等量关系解决如下问题:若
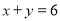 ,
,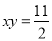 ,则
,则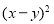 =
= [知识迁移]
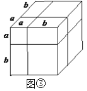
类似地,用两种不同的方法计算同一几何体的体积,也可以得到一个恒等式.
(5)根据图③,写出一个代数恒等式:____________________________;
(6)已知
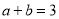 ,
,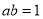 ,利用上面的规律求
,利用上面的规律求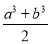 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了更好改善河流的水质,治污公司决定购买10台污水处理设备.现有A,B两种型号的设备,经过市场调查,购买一台
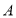 型设备比购买一台
型设备比购买一台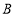 型设备多花费2万元,购买2台A型设备比购买3台B型设备少花费6万元.
型设备多花费2万元,购买2台A型设备比购买3台B型设备少花费6万元.(1)购买一台A型设备、购买一台B型设备各需要多少万元;
(2)治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案.
相关试题

