【题目】如图,在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,点A、C的坐标分别为A(10,0 ),C(0,4),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为( )
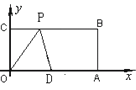
A. (3,4),(2,4) B. (3,4),(2,4),(8,4)
C. (2,4),(8,4) D. (3,4),(2,4),(8,4),(2.5,4)
参考答案:
【答案】B
【解析】试题解析:有两种情况:①以O为圆心,以5为半径画弧交BC于P点,此时OP=OD=5,
在Rt△OPC中,OC=4,OP=5,
由勾股定理得PC=3,
则P的坐标是(3,4);
②以D为圆心,以5为半径画弧交BC于P′和P″点,此时DP′=DP″=OD=5,
过P′作P′N⊥OA于N,
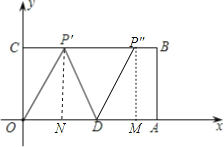
在Rt△OP′N中,设CP′=x,
则DN=5-x,P′N=4,OP=5,由勾股定理得:42+(5-x)2=52,
x=2,
则P′的坐标是(2,4);
过P″作P″M⊥OA于M,
设BP″=a,
则DM=5-a,P″M=4,DP″=5,
在Rt△DP″M中,由勾股定理得:(5-a)2+42=52,
解得:a=2,
∴BP″=2,CP″=10-2=8,
即P″的坐标是(8,4);
假设0P=PD,则由P点向0D边作垂线,交点为Q则有PQ2十QD2=PD2,
∵0P=PD=5=0D,
∴此时的△0PD为正三角形,于是PQ=4,QD=![]() 0D=2.5,PD=5,代入①式,等式不成立.所以排除此种可能.
0D=2.5,PD=5,代入①式,等式不成立.所以排除此种可能.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】大家看过中央电视台“购物街”节目吗?其中有一个游戏环节是大转轮比赛,转轮上平均分布着5、10、15、20一直到100共20个数字.选手依次转动转轮,每个人最多有两次机会.选手转动的数字之和最大不超过100者为胜出;若超过100则成绩无效,称为“爆掉”.
(1)某选手第一次转到了数字5,再转第二次,则他两次数字之和为100的可能性有多大?
(2)现在某选手第一次转到了数字65,若再转第二次了则有可能“爆掉”,请你分析“爆掉”的可能性有多大? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则弧AC的长( ).

A.2π
B.π
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,AC=6,以点A为圆心,AB长为半径画弧DE,若∠1=∠2,则弧DE的长为( )

A.1π
B.1.5π
C.2π
D.3π -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是直线AB上一点,OC平分∠AOB,在直线AB另一侧,以O为顶点作∠DOE=90°.
(1)若∠AOE=48°,则∠BOD=______,∠AOE与∠BOD的关系是_______;
(2)∠AOE与∠COD有什么关系?请写出你的结论,并说明理由.

-
科目: 来源: 题型:
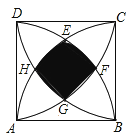
查看答案和解析>>【题目】如图,正方形ABCD的边长为1,分别以顶点A、B、C、D为圆心,1为半径画弧,四条弧交于点E、F、G、H,则图中阴影部分的外围周长为( )
A.
B.
C.π
D.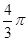
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=15,AC=13,BC边上的高AD=12,则BC的长为________.
相关试题

