搜索
【题目】如图，边长分别为
和
的两个正方形
和
并排放在一起，连结
并延长交
于点
，交
于点
，则
A. 
B. 2 C. 2 D. 1
参考答案：
【答案】B
【解析】
根据正方形的对角线平分一组对角可得∠ADB=∠CGE=45°，再求出∠GDT=45°，从而得到△DGT是等腰直角三角形，根据正方形的边长求出DG，再根据等腰直角三角形的直角边等于斜边的
倍求解即可．
∵BD、GE分别是正方形ABCD，正方形CEFG的对角线，
∴∠ADB=∠CGE=45°，
∴∠GDT=180°-90°-45°=45°，
∴∠DTG=180°-∠GDT-∠CGE=180°-45°-45°=90°，
∴△DGT是等腰直角三角形，
∵两正方形的边长分别为4，8，
∴DG=8-4=4，
∴GT=×4=2
．
故选B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）问题发现：如图1，如果△ACB和△CDE均为等边三角形，点A、D、E在同一直线上，连接BE.则AD与BE的数量关系为 ；∠AEB的度数为 度.
（2）拓展探究：如图2，如果△ACB和△CDE均为等腰三角形，∠ACB=∠DCE=90°，点A、D、E在同一直线上，连接BE，判断线段AE与BE的位置关系，并说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将长方形ABCD沿对角线BD折叠，点C落在点E处，BE交AD于点F，已知∠BDC=62°，则∠DFE的度数为（ ）
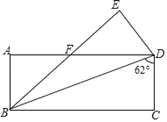
A. 62°B. 56°C. 31°D. 28°
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形ABCD的对角线AC，BD相交于点O，点E，F在BD上，BE=DF．
（1）求证：AE=CF；
（2）若AB=6，∠COD=60°，求矩形ABCD的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】“
年冬季越野赛”在滨河学校操场举行，某运动员从起点学校东门出发，途径湿地公园，沿比赛路线跑回终点学校东门．沿该运动员离开起点的路程
（千米）与跑步时间
（时间）之间的函数关系如图所示，其中从起点到湿地公园的平均速度是
千米/分钟，用时
分钟，根据图像提供的信息，解答下列问题：（
）求图中
的值；（
）组委会在距离起点
千米处设立一个拍摄点
，该运动员从第一次过点
到第二次过点
所用的时间为
分钟．①求
所在直线的函数解析式；②该运动员跑完全程用时多少分钟？
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了参加“醴陵市中小学生首届诗词大会”,某中学八年级的两班学生进行了预选,其中班上前5名学生的成绩(百分制)分别为:八(1)班86,85,77 ,92, 85;八(2)班79 ,85 ,92,85 ,89.通过数据分析,列表如下:
班级
平均分
中位数
众数
方差
八(1)
85
b
c
d
八(2)
a
85
85
e
(1)直接写出表中a,b,c的值：a= ,b= ,c= .
(2)求d,e的值，并根据以上数据分析,你认为哪个班前5名同学的成绩较好?说明理由.
(3)若“醴陵市中小学生首届诗词大会”中，各中学代表队成绩计分分两部分：现场评委记分和网络评委投票记分。且现场评委记分权数为80%，网络评委投票记分权数为20%，请计算A,B,C三所中学代表队的最终得分为多少？
中学A
中学B
中学C
评委记分
90
80
85
网络投票记分
85
92
88
-
科目： 来源： 题型：
查看答案和解析>>【题目】填空并完成以下证明：
已知：点P在直线CD上，∠BAP+∠APD=180°，∠1=∠2．
求证：AB∥CD，∠E=∠F．
证明：∵∠BAP+∠APD=180°，（已知）
∴AB∥ ．（ ）
∴∠BAP= ．（ ）
又∵∠1=∠2，（已知）
∠3= ﹣∠1，
∠4= ﹣∠2，
∴∠3= （等式的性质）
∴AE∥PF．（ ）
∴∠E=∠F．（ ）
相关试题
