【题目】如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )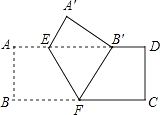
A.12
B.24
C.12 ![]()
D.16 ![]()
参考答案:
【答案】D
【解析】解:在矩形ABCD中,
∵AD∥BC,
∴∠DEF=∠EFB=60°,
∵把矩形ABCD沿EF翻折点B恰好落在AD边的B′处,
∴∠EFB=∠EFB′=60°,∠B=∠A′B′F=90°,∠A=∠A′=90°,AE=A′E=2,AB=A′B′,
在△EFB′中,
∵∠DEF=∠EFB=∠EB′F=60°
∴△EFB′是等边三角形,
Rt△A′EB′中,
∵∠A′B′E=90°﹣60°=30°,
∴B′E=2A′E,而A′E=2,
∴B′E=4,
∴A′B′=2 ![]() ,即AB=2
,即AB=2 ![]() ,
,
∵AE=2,DE=6,
∴AD=AE+DE=2+6=8,
∴矩形ABCD的面积=ABAD=2 ![]() ×8=16
×8=16 ![]() .
.
故选:D
根据平行线的性质和折叠的性质易证得△EFB′是等边三角形,继而可得△A′B′E中,B′E=2A′E,则可求得B′E的长,然后由勾股定理求得A′B′的长,继而求得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分12分)如图,在平面直角坐标系中,抛物线
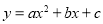 与⊙M相交于A、B、C、D四点.其中AB两点的坐标分别为(-1,0),(0,-2),点D在
与⊙M相交于A、B、C、D四点.其中AB两点的坐标分别为(-1,0),(0,-2),点D在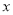 轴上且AD为⊙M的直径.点E是⊙M与
轴上且AD为⊙M的直径.点E是⊙M与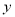 轴的另一个交点,过劣弧
轴的另一个交点,过劣弧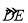 上的点F作FH⊥AD于点H,且FH=1.5.
上的点F作FH⊥AD于点H,且FH=1.5.
(1)求点D的坐标及该抛物线的表达式;
(2)若点P是
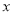 轴上的一个动点,试求出⊿PEF的周长最小时点P的坐标;
轴上的一个动点,试求出⊿PEF的周长最小时点P的坐标;(3)在抛物线的对称轴上是否存在点Q,使⊿QCM是等腰三角形?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)23﹣17﹣(﹣7)+(﹣16);
(2)-5+6÷(-2)×
 ;
;(3)-36×
 ;
;(4)﹣23+|5﹣8|+24÷(﹣3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】“小组合作学习”成为我区推动课堂教学改革,打造自主高效课堂的重要举措.某中学从全校学生中随机抽取100人作为样本,对“小组合作学习”实施前后学生的学习兴趣变化情况进行调查分析,统计如下:
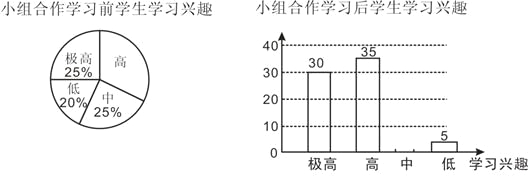
请结合图中信息解答下列问题:
(1)小组合作学习前学生学习兴趣为“高”的所占的百分比为 ;
(2)补全小组合作学习后学生学习兴趣的统计图;
(3)通过“小组合作学习”前后学生学习兴趣的对比,请你估计全校2000名学生中学习兴趣获得提高的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】 (12分)某地电话拨号入网有两种收费方式,用户可以任选其一:
方法一:计时制:0.05元/分;
方法二:包月制:50元/月(限一部个人住宅电话上网).
此外,每一种上网方式都得加收通信费0.02元/分.
(1)设某用户某月上网的时间为
 小时,请你分别写出两种收费方式下该用户应该支付的费用;
小时,请你分别写出两种收费方式下该用户应该支付的费用;(2)若某用户估计一个月内上网的时间为20小时,你认为采用哪种方式较为合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形
D.当AC=BD时,它是正方形 -
科目: 来源: 题型:
查看答案和解析>>【题目】我区某校分别于2014年、2015年随机调查相同数量的学生,对数学课开展小组合作学习的情况进行调查(开展情况分为较少、有时、常常、总是四种),绘制成部分统计图如下.请根据图中信息,解答下列问题:
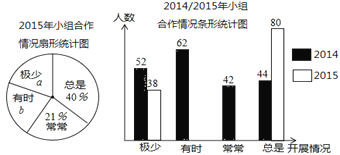
(1)a= %,b= %,“总是”对应阴影的圆心角为 °;
(2)请你补全条形统计图;
(3)若该校2015年共有1200名学生,请你统计其中认为数学课“总是”开展小组合作学习的学生有多少名?
(4)数学课开展小组合作学习的情况有何变化?
相关试题

