【题目】如图,菱形ABCD周长为8,∠BAD=120°,P为BD上一动点,E为CD中点,则PE+PC的最小值长为 .

参考答案:
【答案】
【解析】
试题分析:先求出菱形各边的长度,作点E关于直线BD的对称点E′,连接CE′交BD于点P,则CE′的长即为PE+PC的最小值,由菱形的性质可知E′为AD的中点,由直角三角形的判定定理可得出△DCE′是直角三角形,利用勾股定理即可求出CE′的长.
解:∵菱形ABCD的周长为8,
∴AD=DC=2,
作点E关于直线BD的对称点E′,连接CE′交BD于点P,则CE′的长即为PE+PC的最小值,
∵四边形ABCD是菱形,
∴BD是∠ADC的平分线,
∴E′在AD上,由图形对称的性质可知,DE=DE′=![]() AD=
AD=![]() ×2=1,
×2=1,
∵DE′=DE=![]() DC,
DC,
∴△DCE′是直角三角形,
∴CE′=![]() =
=![]() =
=![]() ,
,
故PE+PC的最小值是![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若am=6,an=3,则am+2n的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】按图填空, 并注明理由
已知: 如图, ∠1=∠2, ∠3=∠E. 求证: AD∥BE
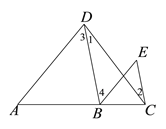
证明: ∵∠1 = ∠2 (已知)
∴ ∥ ( )
∴ ∠E = ∠ ( )
又∵ ∠E = ∠3 ( 已知 )
∴ ∠3 = ∠ ( 等量代换 )
∴ ∥ ( 内错角相等,两直线平行 )
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
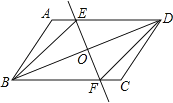
(1)求证:△DOE≌△BOF;
(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A1B1C,连结AA1,若∠AA1B1=15°,则∠B的度数是 .
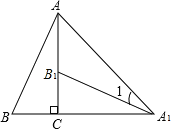
-
科目: 来源: 题型:
查看答案和解析>>【题目】居民区内的“广场舞”引起媒体关注,某都市频道媒体为此进行过专访报道,小平想了解本小区居民对“广场舞”的看法,进行了一次抽样调查,把居民对“广场舞”的看法分为四个层次:A.非常赞同;B.赞同但要有时间限制;C.无所谓;D.不赞同.并将调查结果绘制了图1和图2两幅不完整的统计图.
请你根据图中提供的信息解答下列问题:

(1)求本次被抽查的居民有多少人?
(2)将图1和图2补充完整;
(3)求图2中“C”层次所在扇形的圆心角的度数;
(4)估计该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有多少人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解一元二次方程x2+4x﹣5=0,此方程可变形为( )
A. (x+2)2=9 B. (x﹣2)2=9 C. (x+2)2=1 D. (x﹣2)2=1
相关试题

