【题目】如图,点O是线段AB上的一点,OA=OC,OD平分∠AOC交AC于点D,OF平分∠COB,CF⊥OF于点F.
(1)求证:四边形CDOF是矩形;
(2)当∠AOC多少度时,四边形CDOF是正方形?并说明理由.
参考答案:
【答案】
(1)证明:∵OD平分∠AOC,OF平分∠COB(已知),
∴∠AOC=2∠COD,∠COB=2∠COF。
∵∠AOC+∠BOC=180°,∴2∠COD+2∠COF=180°。∴∠COD+∠COF=90°。
∴∠DOF=90°。
∵OA=OC,OD平分∠AOC(已知)。
∴OD⊥AC,AD=DC(等腰三角形的“三合一”的性质)。∴∠CDO=90°。
∵CF⊥OF,∴∠CFO=90°。
∴四边形CDOF是矩形。
(2)解:当∠AOC=90°时,四边形CDOF是正方形。理由如下:
∵∠AOC=90°,AD=DC,∴OD=DC。
又由(1)知四边形CDOF是矩形,则四边形CDOF是正方形。
因此,当∠AOC=90°时,四边形CDOF是正方形。
【解析】(1)根据角平分线的定义得到∠DOF=90°,根据等腰三角形的性质三线合一,得到∠CDO=90°,再由CF⊥OF,得到四边形CDOF是矩形;(2)根据正方形的判定方法有一组临边相等的矩形是正方形,当∠AOC=90°时OD=DC,得到四边形CDOF是正方形.
【考点精析】本题主要考查了正方形的判定方法的相关知识点,需要掌握先判定一个四边形是矩形,再判定出有一组邻边相等;先判定一个四边形是菱形,再判定出有一个角是直角才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂有甲种原料
 ,乙种原料
,乙种原料 ,现用两种原料生产处
,现用两种原料生产处 两种产品共
两种产品共 件,已知生产每件
件,已知生产每件 产品需甲种原料
产品需甲种原料 ,乙种原料
,乙种原料 ,且每件
,且每件 产品可获得
产品可获得 元;生产每件
元;生产每件 产品甲种原料
产品甲种原料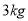 ,乙种原料
,乙种原料 ,且每件
,且每件 产品可获利润
产品可获利润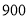 元,设生产
元,设生产 产品
产品 件(产品件数为整数件),根据以上信息解答下列问题:
件(产品件数为整数件),根据以上信息解答下列问题:(1)生产
 两种产品的方案有哪几种?
两种产品的方案有哪几种?(2)设生产这
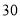 件产品可获利
件产品可获利 元,写出关于
元,写出关于 的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
的函数解析式,写出(1)中利润最大的方案,并求出最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上A,B两点,点A对应的数为3,若线段AB的长为5,则点B对应的数为( )
A.-2B.5C.-2或8D.8
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A.16的算术平方根是-4B.25的平方根是5
C.-8的立方根是-2D.1的立方根是1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果△ABC≌△DEF,△DEF周长是30 cm,DE=9 cm,EF=13 cm.∠E=∠B,则AC=__________cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在创建“全国园林城市”期间,郴州市某中学组织共青团员去植树,其中七位同学植树的棵树分别为:3,1,1,3,2,3,2,这组数据的中位数和众数分别是( )
A.3,2
B.2,3
C.2,2
D.3,3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P位于第二象限,距y轴3个单位长度,距x轴4个单位长度,则点P的坐标是( )
A. (-3,4)B. (3,-4)C. (4,-3)D. (-4,3)
相关试题

