【题目】如图1,已知抛物线的方程C1: ![]() (m>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
(m>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
(1)若抛物线C1过点M(2, 2),求实数m的值;
(2)在(1)的条件下,求△BCE的面积;
(3)在(1)的条件下,在抛物线的对称轴上找一点H,使得BH+EH最小,求出点H的坐标;
(4)在第四象限内,抛物线C1上是否存在点F,使得以点B、C、F为顶点的三角形与△BCE相似?若存在,求m的值;若不存在,请说明理由.

参考答案:
【答案】(1)![]() ;(2)6;(3)
;(2)6;(3) ![]() ;(4)
;(4) ![]() .
.
【解析】试题分析:(1)把M(2,2)代入函数解析式即可;(2)把![]() 代回函数解析式,求出点B、C、E的坐标即可;(3)连接CE交对称轴与点H,此时BH+EH的值最小;(4)①过点B作EC的平行线交抛物线于F,过点F作FF′⊥x轴于F′.由于∠BCE=∠FBC△BCE∽△FBC,②作∠CBF=45°交抛物线于F,过点F作FF′⊥x轴于F′,由于∠EBC=∠CBF,△BCE∽△BFC
代回函数解析式,求出点B、C、E的坐标即可;(3)连接CE交对称轴与点H,此时BH+EH的值最小;(4)①过点B作EC的平行线交抛物线于F,过点F作FF′⊥x轴于F′.由于∠BCE=∠FBC△BCE∽△FBC,②作∠CBF=45°交抛物线于F,过点F作FF′⊥x轴于F′,由于∠EBC=∠CBF,△BCE∽△BFC
试题解析:(1)将M(2, 2)代入![]() ,得
,得![]() .解得
.解得![]() .
.
(2)当![]() 时,
时, ![]() .所以C(4, 0),E(0, 2),B(-2,0).
.所以C(4, 0),E(0, 2),B(-2,0).
所以S△BCE=![]() .
.
(3)如图2,抛物线的对称轴是直线x=1,当H落在线段EC上时,BH+EH最小.
设对称轴与x轴的交点为P,那么![]() .
.
因此![]() .解得
.解得![]() .所以点H的坐标为
.所以点H的坐标为![]() .
.
(4)①如图3,过点B作EC的平行线交抛物线于F,过点F作FF′⊥x轴于F′.
由于∠BCE=∠FBC,所以当![]() ,即
,即![]() 时,△BCE∽△FBC.
时,△BCE∽△FBC.
设点F的坐标为![]() ,由
,由![]() ,得
,得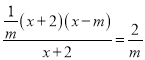 .
.
解得x=m+2.所以F′(m+2, 0).
由![]() ,得
,得![]() .所以
.所以![]() .
.
由![]() ,得
,得![]() .
.
整理,得0=16.此方程无解.
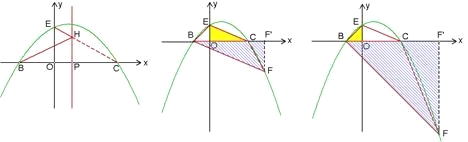
图2 图3 图4
②如图4,作∠CBF=45°交抛物线于F,过点F作FF′⊥x轴于F′,
由于∠EBC=∠CBF,所以![]() ,即
,即![]() 时,△BCE∽△BFC.
时,△BCE∽△BFC.
在Rt△BFF′中,由FF′=BF′,得![]() .
.
解得x=2m.所以F′![]() .所以BF′=2m+2,
.所以BF′=2m+2, ![]() .
.
由![]() ,得
,得![]() .解得
.解得![]() .
.
综合①、②,符合题意的m为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB=BC,∠ABC=90°,以AB为直径的⊙O交OC与点D,AD的延长线交BC于点E,过D作⊙O的切线交BC于点F.下列结论:①CD2=CE·CB;②4EF 2=ED ·EA;③∠OCB=∠EAB;④
 .其中正确的只有____________________.(填序号)
.其中正确的只有____________________.(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,直径AB⊥CD,垂足为E,点M在OC上,AM的延长线交⊙O于点G,交过C的直线于F,∠1=∠2,连结CB与DG交于点N.
(1)求证:CF是⊙O的切线;
(2)求证:△ACM∽△DCN;
(3)若点M是CO的中点,⊙O的半径为4,cos∠BOC=
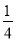 ,求BN的长.
,求BN的长.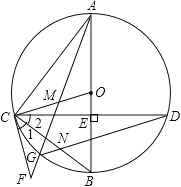
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个圆内接四边形ABCD中,已知∠A=100°,则∠C的度数为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为支援灾区,某校爱心活动小组准备用筹集的资金购买A、B两种型号的学习用品共1000件.已知B型学习用品的单价比A型学习用品的单价多10元,用180元购买B型学习用品的件数与用120元购买A型学习用品的件数相同.
(1)求A、B两种学习用品的单价各是多少元?
(2)若购买这批学习用品的费用不超过28000元,则最多购买B型学习用品多少件? -
科目: 来源: 题型:
查看答案和解析>>【题目】减负提质“1+5”行动计划是我市教育改革的一项重要举措.某中学“阅读与演讲社团”为了了解本校学生的每周课外阅读时间,采用随机抽样的方式进行了问卷调查,调查结果分为“2小时以内”、“2小时~3小时”、“3小时~4小时”和“4小时以上”四个等级,分别用A、B、C、D表示,根据调查结果绘制成了如图所示的两幅不完整的统计图.由图中所给出的信息解答下列问题:
(1)求出x的值,并将不完整的条形图补充完整;
(2)在此次调查活动中,初三(1)班的两个学习小组内各有2人每周课外阅读时间都是4小时以上,现从这4人中任选2人去参加学校的知识抢答赛.用列表或画树状图的方法求选出的2人来自不同小组的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=(k﹣3)x2+2x+1的图象与x轴有交点,则k的取值范围为 .
相关试题

