【题目】某中学为了了解学生对手机的依赖程度,开展了一次“学生周末手机使用时间”抽样调查,根据调查结果绘制了如下两种不完整的统计图表.
组别 | 周末手机使用时间 | 人数 |
|
| 20 |
|
|
|
|
| 22 |
|
| 10 |
|
| 8 |
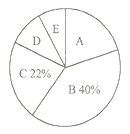
请根据图表信息解答下列问题:
(1)本次抽样,共调查了 人;
(2)扇形统计图中“![]() ”所对应的圆心角的度数是/span> ;
”所对应的圆心角的度数是/span> ;
(3)估计该校2450名学生中周末手机使用时间小于2小时的人数.
参考答案:
【答案】(1)100;(2)![]() ;(3)该校周末使用手机时间小于2小时的学生有1470人.
;(3)该校周末使用手机时间小于2小时的学生有1470人.
【解析】
(1)由等级C的人数除以占的百分比,得出调查总人数即可,进而确定出等级B与等级D的人数,进而求出m与n的值;
(2)由D占的百分比,乘以360即可得到结果;
(3)根据题意列式计算即可得到结论.
(1)22÷22%=100人,
答:本次抽样,共调查了100人,
故答案为:100;
(2)扇形统计图中“D”所对应的圆心角的度数是![]() ×360°=36°,
×360°=36°,
故答案为:36°;
(3)m=100×40%=40人,
2450×![]() =1715人,
=1715人,
答:估计该校2450名学生中,周末手机使用时间小于2小时的人数为1715人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于E,过点E作EG⊥AC于G,交BC的延长线于F.
(1)求证:AE=BE;
(2)求证:FE是⊙O的切线;
(3)若FE=4,FC=2,求⊙O的半径及CG的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了更好改善河流的水质,治污公司决定购买10台污水处理设备.现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
A型
B型
价格(万元/台)
a
b
处理污水量(吨/月)
240
180
(1)求a,b的值;
(2)治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于某一函数给出如下定义:若存在实数p,当其自变量的值为p时,其函数值等于p,则称p为这个函数的不变值.在函数存在不变值时,该函数的最大不变值与最小不变值之差q称为这个函数的不变长度.特别地,当函数只有一个不变值时,其不变长度q为零.例如:下图中的函数有0,1两个不变值,其不变长度q等于1.
(1)分别判断函数y=x-1,y=x-1,y=x2有没有不变值?如果有,直接写出其不变长度;
(2)函数y=2x2-bx.
①若其不变长度为零,求b的值;
②若1≤b≤3,求其不变长度q的取值范围;
(3) 记函数y=x2-2x(x≥m)的图象为G1,将G1沿x=m翻折后得到的函数图象记为G2,函数G的图象由G1和G2两部分组成,若其不变长度q满足0≤q≤3,则m的取值范围为 .
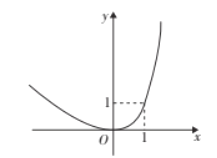
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是菱形ABCD的对角线AC上一动点,过P作垂直于AC的直线交菱形ABCD的边于M、N两点,设AC=2,BD=1,AP=x,则△AMN的面积为y,则y关于x的函数图象的大致形状是( )

A.
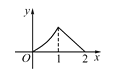 B.
B. 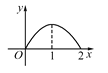
C.
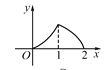 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1所示的三棱柱,高为
 ,底面是一个边长为
,底面是一个边长为 的等边三角形.
的等边三角形.(1)这个三棱柱有 条棱,有 个面;
(2)图2方框中的图形是该三棱柱的表面展开图的一部分,请将它补全;
(3)要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,需剪开 条棱,需剪开棱的棱长的和的最大值为
 .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点A1,A2,A3,A4和C1,C2,C3,C4分别是ABCD的五等分点,点B1,B2和D1,D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为2,则平行四边形ABCD的面积为( )

A. 4 B.
 C.
C.  D. 30
D. 30
相关试题

