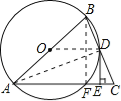
【题目】如图,在△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥AC,垂足为E,⊙O经过A,B,D三点.
(1)求证:AB是⊙O的直径;
(2)判断DE与⊙O的位置关系,并加以证明;
(3)若⊙O的半径为3,∠BAC=60°,求DE的长.

参考答案:
【答案】(1)证明见解析;(2)DE与圆O相切;(3)![]() .
.
【解析】试题分析:(1)连接AD,根据等腰三角形三线合一性质得到AD⊥BC,再根据90°的圆周角所对的弦为直径即可证得AB是⊙O的直径;(2)DE与圆O相切,理由为:连接OD,利用中位线定理得到OD∥AC,利用两直线平行内错角相等得到∠ODE为直角,再由OD为半径,即可得证;(3)由AB=AC,且∠BAC=60°,得到DABC为等边三角形,连接BF,DE为DCBF中位线,求出BF的长,即可确定出DE的长.
试题解析:(1)证明:连接AD,∵AB=AC,BD=DC,∴AD⊥BC,∴∠ADB=90°,∴AB为⊙O的直径;(2)DE与⊙O相切,理由为:连接OD,∵O、D分别为AB、BC的中点,∴OD为△ABC的中位线,∴OD∥BC,∵DE⊥BC,∴DE⊥OD,∵OD为⊙O的半径,∴DE与⊙O相切;(3)解:连接BF,∵AB=AC,∠BAC=60°,∴△ABC为等边三角形,∴AB=AC=BC=6,∵AB为⊙O的直径,∴∠AFB=∠DEC=90°,∴AF=CF=3,DE∥BF,∵D为BC中点,∴E为CF中点,DE=![]() BF,在Rt△ABF中,∠AFB=90°,AB=6,AF=3,∴BF=
BF,在Rt△ABF中,∠AFB=90°,AB=6,AF=3,∴BF=![]() ,则DE=
,则DE=![]() BF=
BF=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:a+a=( )
A.2
B.a2
C.2a2
D.2a -
科目: 来源: 题型:
查看答案和解析>>【题目】对于算式20203﹣2020,下列说法错误的是( )
A.能被2019整除B.能被2020整除C.能被2021整除D.能被2022整除
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:m2m5=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地区两个城市之间,可乘坐普通列车或高铁.已知高铁行驶线路的路程是400千米,普通列车行驶线路的路程是高铁行驶路程的1.3倍;高铁的平均速度是普通列车平均速度的2.5倍。如果乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求高铁的平均速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米,
 ≈1.73)
≈1.73)
-
科目: 来源: 题型:
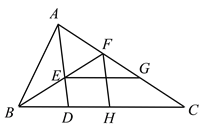
查看答案和解析>>【题目】如图,△ABC中, ∠BAC=∠ADB,BE平分∠ABC交AD于点E,H为BC上一点,且BH=BA交AC于点F,连接FH.
⑴求证:AE=FH;
⑵作EG//BC交AC于点G若AG=5,AC=8,求FG的长.
相关试题

