【题目】如图,抛物线经过A(﹣1,0),B(5,0),C(0,- ![]() )三点.
)三点.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:设抛物线的解析式为y=ax2+bx+c(a≠0),
∵A(﹣1,0),B(5,0),C(0,- ![]() )三点在抛物线上,
)三点在抛物线上,
∴ 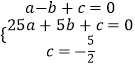 ,
,
解得 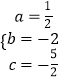 .
.
∴抛物线的解析式为:y= ![]() x2﹣2x﹣
x2﹣2x﹣ ![]()
(2)
解:∵抛物线的解析式为:y= ![]() x2﹣2x﹣
x2﹣2x﹣ ![]() ,
,
∴其对称轴为直线x=﹣ ![]() =﹣
=﹣ ![]() =2,
=2,
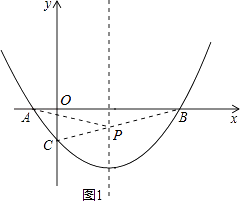
连接BC,如图1所示,
∵B(5,0),C(0,﹣ ![]() ),
),
∴设直线BC的解析式为y=kx+b(k≠0),
∴ 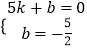 ,
,
解得 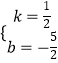 ,
,
∴直线BC的解析式为y= ![]() x﹣
x﹣ ![]() ,
,
当x=2时,y=1﹣ ![]() =﹣
=﹣ ![]() ,
,
∴P(2,﹣ ![]() )
)
(3)
解:存在.
如图2所示,
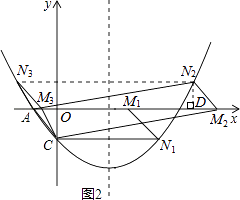
①当点N在x轴下方时,
∵抛物线的对称轴为直线x=2,C(0,﹣ ![]() ),
),
∴N1(4,﹣ ![]() );
);
②当点N在x轴上方时,
如图,过点N2作N2D⊥x轴于点D,
在△AN2D与△M2CO中,
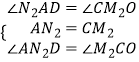
∴△AN2D≌△M2CO(ASA),
∴N2D=OC= ![]() ,即N2点的纵坐标为
,即N2点的纵坐标为 ![]() .
.
∴ ![]() x2﹣2x﹣
x2﹣2x﹣ ![]() =
= ![]() ,
,
解得x=2+ ![]() 或x=2﹣
或x=2﹣ ![]() ,
,
∴N2(2+ ![]() ,
, ![]() ),N3(2﹣
),N3(2﹣ ![]() ,
, ![]() ).
).
综上所述,符合条件的点N的坐标为(4,﹣ ![]() ),(2+
),(2+ ![]() ,
, ![]() )或(2﹣
)或(2﹣ ![]() ,
, ![]() ).
).
【解析】(1)设抛物线的解析式为y=ax2+bx+c(a≠0),再把A(﹣1,0),B(5,0),C(0,- ![]() )三点代入求出a、b、c的值即可;(2)因为点A关于对称轴对称的点B的坐标为(5,0),连接BC交对称轴直线于点P,求出P点坐标即可;(3)分点N在x轴下方或上方两种情况进行讨论.
)三点代入求出a、b、c的值即可;(2)因为点A关于对称轴对称的点B的坐标为(5,0),连接BC交对称轴直线于点P,求出P点坐标即可;(3)分点N在x轴下方或上方两种情况进行讨论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,D是BC边上一点∠1=∠2,∠3=∠4,∠BAC=69°,求∠DAC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知AD,AE分别是△ADC和△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°.试求:
(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列条件中,不能证明△ABC≌△DCB是 ( )

A. AB=DC,AC=DB B. AB=DC,∠ABC=∠DCB
C. DB=AC,∠DBC=∠ACB D. DC=AB,∠DBC=∠ACB
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算不正确的是( )
A.
B.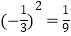
C.|3|=3
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=40°,∠C=80°,AD是BC边上的高,AE平分∠BAC.
(1)求∠BAE的度数;(2)求∠DAE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的3个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点B顺时针旋转到△A′BC′的位置,且点A′、C′仍落在格点上,则线段AB扫过的图形面积是平方单位(结果保留π).

相关试题

