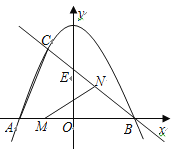
【题目】如图,抛物线![]() 与x轴交于点A、点B,与直线
与x轴交于点A、点B,与直线![]() 相交于点B、点C,直线
相交于点B、点C,直线![]() 与y轴交于点E。
与y轴交于点E。
(1)写出直线BC的解析式。
(2)求△ABC的面积。
(3)若点M在线段AB上以每秒1个单位长度的速度从A向B运动(不与A,B重合),同时,点N在射线BC上以每秒2个单位长度的速度从B向C运动。设运动时间为t秒,请写出△MNB的面积S与t的函数关系式,并求出点M运动多少时间时,△MNB的面积最大,最大面积是多少?
参考答案:
【答案】
【解析】
试题分析:(1)根据待定系数法求出BC的解析式;
(2)令y=0代入y=-![]() x2+3求出点A,B的坐标.把B点坐标代入y=-
x2+3求出点A,B的坐标.把B点坐标代入y=-![]() x+b求出BC的解析式,联立方程组求出B.C的坐标.求出AB,CD的长后可求出三角形ABC的面积.
x+b求出BC的解析式,联立方程组求出B.C的坐标.求出AB,CD的长后可求出三角形ABC的面积.
(3)过N点作NP⊥MB,证明△BNP∽△BEO,由已知令y=0求出点E的坐标,利用线段比求出NP,BE的长.求出S与t的函数关系式后利用二次函数的性质求出S的最大值.
试题解析:(1)在![]() 中,令y=0
中,令y=0
∴![]()
∴x1=2,x2=-2
∴A(-2,0),B(2,0)
又∵点B在![]() 上
上
∴![]()
![]()
∴BC的解析式为![]()
(2)由 ![]()

得 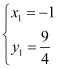 ;
; 
∴C ![]() B(2,0)
B(2,0)
∴AB=4 CD=![]()
∴S△ABC=![]()
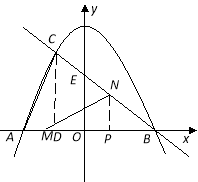
(3)过点N作NP⊥MB于点P
∵EO⊥MB
∴NP∥EO
∴△BNP∽△BEO
∴![]()
由直线![]() 可得:E
可得:E![]()
∴在RT△BEO中,BO=2,EO=![]() ,则BE=
,则BE=![]()
∴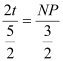
∴NP=![]()
∴S=![]()
![]()
S=![]()
S=![]()
∵![]() <0
<0
∴当t =2时,S最大=![]()
∴当点M运动2秒时,△MNB的面积达到最大,最大为![]() 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将
 ABCD的边AB延长到点E,使BE=AB,连接DE,交边BC于点F.
ABCD的边AB延长到点E,使BE=AB,连接DE,交边BC于点F.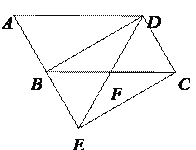
(1)求证:△BEF≌△CDF.
(2)连接BD,CE,若∠BFD=2∠A,求证四边形BECD是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.5ab﹣3b=2aB.2a2b÷b=2a2(b≠0)
C.(a﹣1)2=a2﹣1D.(﹣3a2b)2=6a4b2
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=3x2﹣2的顶点坐标是( )
A.(3,﹣2)B.(﹣3,2)C.(0,﹣2)D.(3,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,对角线AC上有一点P,连接BP、DP,过点P作PE⊥PB交CD于点E,连接BE.

(1)求证:BP=EP;
(2)若CE=3,BE=6,求∠CPE的度数;
(3)探究AP、PC、BE之间的数量关系,并给予证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中心对称图形的旋转角是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面运算正确的是( )
A. (x+2)2=x2+4 B. (x-1)(-1-x)=x2-1
C. (-2x+1)2=4x2+4x+1 D. (x-1)(x-2)=x2-3x+2
相关试题

