搜索
【题目】科学研究发现，空气含氧量y（克/立方米）与海拔高度x（米）之间近似地满足一次函数关系．经测量，在海拔高度为1000米的地方，空气含氧量约为267克/立方米；在海拔高度为2000米的地方，空气含氧量约为235克/立方米．
（1）求出y与x的函数表达式；
（2）求出海拔高度为0米的地方的空气含氧量．
参考答案：
【答案】（1）
；（2）该山山顶处的空气含氧量约为299克/立方米.
【解析】
（1）设出一次函数的解析式，利用在海拔高度为1000米的地方，空气含氧量约为267克/立方米；在海拔高度为2000米的地方，空气含氧量约为235克/立方米，代入解析式求出即可；
（2）根据某山的海拔高度为0米，代入（1）中解析式，求出即可．
解：（1）设y＝kx+b（k≠0），则有：
，
解得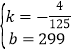
，
故y＝
x+299；
（2）当x＝0时，y＝299（克/立方米）．
答：该山山顶处的空气含氧量约为299克/立方米．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，BE是线段AB的延长线，且∠CBE=∠A=∠C．
（1）由∠CBE=∠A可以判断____∥_____，根据是_____________；
（2）由∠CBE=∠C可以判断____∥_____，根据是_____________．
-
科目： 来源： 题型：
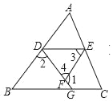
查看答案和解析>>【题目】如图，已知∠1+∠2＝180°，∠3＝∠B，试判断DE与BC的位置关系，并对结论进行说理．
证明：DE∥BC．
理由如下：
∵∠1+∠2＝180°（已知）
∠1+∠4＝180°（平角定义）
∴∠2＝∠4（同角的补角相等）
∴ ∥ （ ）
∴∠3+ ＝180°（ ）
∵∠3＝∠B（已知）
∴∠B+ ＝180°（等量代换）
∴ ∥ （ ）
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了解某校学生的身高情况，随机抽取该校男生、女生进行抽样调查．已知抽取的样本中，男生、女生的人数相同，利用所得数据绘制如下统计图表：
身高情况分组表（单位：cm）
组别
身高
A
x＜155
B
155≤x＜160
C
160≤x＜165
D
165≤x＜170
E
x≥170
根据图表提供的信息，回答下列问题：
（1）样本中，男生的身高众数在 组，中位数在 组；
（2）样本中，女生身高在E组的人数有 人；
（3）已知该校共有男生400人，女生380人，请估计身高在160≤x＜170之间的学生约有多少人？
-
科目： 来源： 题型：
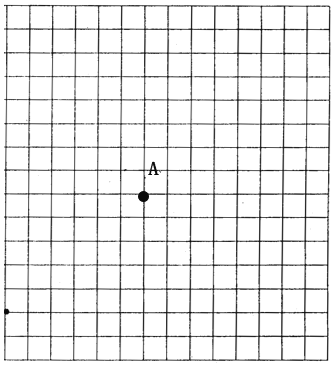
查看答案和解析>>【题目】在A市正北300km处有B市，(1)以A市为原点，东西方向的直线为x轴，南北方向的直线为y轴，并以100km为1个单位建立平面直角坐标系．
(2)根据气象台预报，今年7号台风中心位置现在C(5，2)处，并以60千米/时的速度自东向西移动，台风影响范围半径为200km，问经几小时后，B市将受到台风影响?并画出示意图．
-
科目： 来源： 题型：
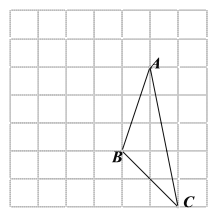
查看答案和解析>>【题目】画图（只能借助于网格）并填空：
如图，每个小正方形的边长为
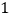个单位，每个小正方形的顶点叫格点.（1）将
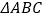向左平移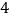
格，再向上平移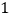格，请在图中画出平移后的
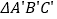；（2）
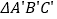的面积为 ；（3）利用网格在图中画出△ABC的中线
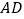，高线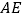
；（4）在图中能使
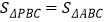的格点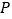
的个数有 个(点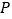异于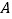
).
-
科目： 来源： 题型：
查看答案和解析>>【题目】把不等式组
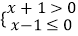的解集表示在数轴上，正确的是（ ）
A.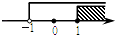
B.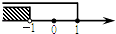
C.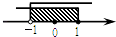
D.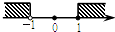
相关试题
