搜索
【题目】设A（-2，y1），B（1，y2），C（2，y3）是抛物线y=-（x+1）2+a上的三点，则y1 ， y2 ， y3的大小关系为（ ）
A.y1>y2>y3
B.y1>y3>y2
C.y3>y2>y1
D.y3>y1>y2
参考答案：
【答案】A
【解析】∵函数的解析式是y=-（x+1）2+a，如右图，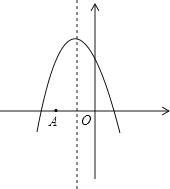
∴对称轴是x=-1，
∴点A关于对称轴的点A′是（0，y1），
那么点A′、B、C都在对称轴的右边，而对称轴右边y随x的增大而减小，
于是y1＞y2＞y3 ．
故选A．
【考点精析】认真审题，首先需要了解二次函数的性质(增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
， 
， 
于
， 
于
．
求证：
．证明：在
和
中，
∴
≌
（ ）．∴
__________
__________（ ）．∴
是
的角平分线．又∵
于
， 
于
，∴
（ ）． -
科目： 来源： 题型：
查看答案和解析>>【题目】将抛物线y=3x2向上平移3个单位，再向左平移2个单位，那么得到的抛物线的解析式为（ ）
A.y=3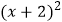
+3
B.y=3
+3
C.y=3-3
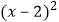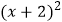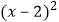D.y=3-3 -
科目： 来源： 题型：
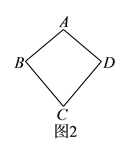
查看答案和解析>>【题目】从图
所示的风筝中可以抽象出几何图形，我们把这种几何图形叫做“筝形”．具体定义如下：如图
，在四边形
中，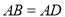 
， 
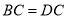，我们把这种两组邻边分别相等的四边形叫做“筝形”．
（
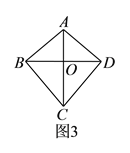
）结合图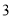
，通过观察、测量、折纸，可以猜想“筝形”具有诸如“
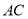平分
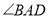和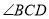
”这样的性质，请结合图形，再写出两条“筝形”的性质．①____________________________．
②____________________________．
（
）从你写出的两条性质中，任选一条“筝形”的性质给出证明． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数y=a（x-2）2+c（a＞0），当自变量x分别取
、3、0时，对应的函数值分别：y1 ， y2 ， y3 ， 则y1 ， y2 ， y3的大小关系正确的是（ ）
A.y3<y2<y1
B.y1<y2<y3
C.y2<y1<y3
D.y3<y1<y2 -
科目： 来源： 题型：
查看答案和解析>>【题目】下列多项式中能用平方差公式分解的有（ ）
①﹣a2﹣b2；②9x2﹣4y2；③x2﹣4y2；④（﹣m）2﹣（﹣n）2；
⑤﹣144a2+121b2；⑥﹣
m2+2n2．A. 1个 B. 2个 C. 3个 D. 5个
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，阴影部分是边长为a的大正方形中剪去一个边长为b的小正方形后所得到的图形，将阴影部分通过割、拼，形成新的图形，给出下列3种割拼方法，其中能够验证平方差公式的是( )
A. ①② B. ②③ C. ①③ D. ①②③
相关试题
