【题目】已知:如图,AB∥DC,AC和BD相交于点O,E是CD上一点,F是OD上一点,且∠1=∠A.
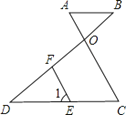
(1)求证:FE∥OC;(2)若∠B=40°,∠1=60°,求∠OFE的度数.
参考答案:
【答案】(1)证明见解析;(2)∠OFE=100°.
【解析】试题分析:
(1)由AB∥CD可得∠A=∠C,再由∠1=∠A,可得∠1=∠C,从而可得FE∥OC;
(2)由AB∥CD可得∠D=∠B=40°,结合∠1=60°,由三角形外角的性质可得∠OFE=100°.
试题解析:
(1)∵AB∥DC(已知),
∴∠A=∠C(两直线平行,内错角相等),
∵∠1=∠A(已知),
∴∠1=∠C(等量代换),
∴FE∥OC(同位角相等,两直线平行).
(2)∵AB∥DC,
∴∠D=∠B,
∵∠B=40°,
∴∠D=40°,
∵∠OFE是△DEF的外角,
∴∠OFE=∠D+∠1,
∵∠1=60°,
∴∠OFE=40°+60°=100°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2017次运动后,动点P的坐标是______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板按如图方式摆放,两个直角顶点重合,∠A=60°,∠E=∠B=45°.
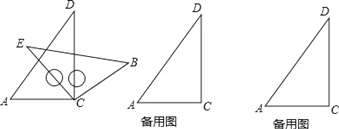
(1)求证:∠ACE=∠BCD;
(2)猜想∠ACB与∠ECD数量关系并说明理由;
(3)按住三角板ACD不动,绕点C旋转三角板ECB,探究当∠ACB等于多少度时,AD∥CB.请在备用图中画出示意图并简要说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个角是20°10′,则它的余角是
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,DE垂直平分AB,D为垂足交AC于E.
(1)若∠A=50°,求∠EBC的度数;
(2)若
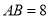 ,△BEC的周长是11,求ABC的周长.
,△BEC的周长是11,求ABC的周长. 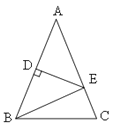
-
科目: 来源: 题型:
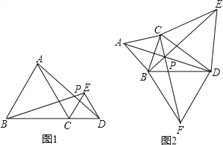
查看答案和解析>>【题目】(1)如图1,△ABC和△CDE都是等边三角形,且B、C、D三点共线,联结AD、BE相交于点P,求证:BE=AD;
(2)如图2,在△BCD中,∠BCD<120°,分别以BC、CD和BD为边在△BCD外部作等边三角形ABC、等边三角形CDE和等边三角形BDF,联结AD、BE和CF交于点P,下列结论中正确的是_________(只填序号即可)
①AD=BE=CF;②∠BEC=∠ADC;③∠DPE=∠EPC=∠CPA=60°;
(3)如图2,在(2)的条件下,求证:PB+PC+PD=BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式2x≥x+2的解集为( )
A. x>2B. x<2C. x≥2D. x≤2
相关试题

