【题目】某物流公司引进A、B两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,A种与某日0时开始搬运,过了1小时,B种机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(千克)与时间x(时)的函数图象,线段EF表示B种机器人的搬运量yB(千克)与时间x(时)的函数图象.根据图象提供的信息,解答下列问题: 
(1)求yB关于x的函数解析式;
(2)如果A、B两种机器人连续搬运5个小时,那么B种机器人多搬运了多少千克?
参考答案:
【答案】
(1)解:设yB关于x的函数解析式是yB=kx+b,
![]() ,得
,得 ![]() ,
,
答:yB关于x的函数解析式是yB=90x﹣90(1≤k≤6);
(2)解:由图象可得,
A种机器人屠呦呦的速度为:180÷3=60千克/小时,
B种机器人的速度为:180÷(3﹣1)=90千克/小时,
∴A、B两种机器人连续搬运5个小时,B种机器人多搬运了(90﹣60)×5=150(千克),
答:A、B两种机器人连续搬运5个小时,那么B种机器人多搬运了150千克.
【解析】(1)根据函数图象可以求得yB关于x的函数解析式;(2)根据函数图象可以去的两种机器人的速度,从而可以求得A、B两种机器人连续搬运5个小时,B种机器人多搬运了多少千克.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知2xayb与﹣7xb﹣3y4是同类项,则ab= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A在函数
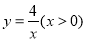 图像上,过点A作x轴和y轴的平行线分别交函数
图像上,过点A作x轴和y轴的平行线分别交函数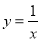 图像于点B、C,直线BC与坐标轴的交点为D、E.当点A在函数
图像于点B、C,直线BC与坐标轴的交点为D、E.当点A在函数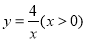 图像上运动时,
图像上运动时,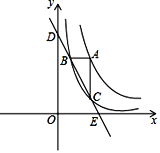
(1)设点A横坐标为a,则点B的坐标为 ,点C的坐标为 (用含a的字母表示);
(2)△ABC的面积是否发生变化?若不变,求出△ABC的面积,若变化,请说明理由;
(3)请直接写出BD与CE满足的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形纸片ABCD中,AD=5,AB=3,点E为BC上一点,沿着AE剪下△ABE,将它平移至△DCE'的位置,拼成四边形AEE'D.

(1)当点E与点B的距离是多少时,四边形AEE'D是菱形?并说明理由;
(2)在(1)的条件下,求菱形AEE'D的两条对角线的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣2x﹣6=0的两个根为x1,x2,则x1+x2=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A1(a1,a2),A2(a2,a3),A3(a3,a4),…,An(an,an+1)(n为正整数)都在一次函数y=x+3的图象上.若a1=2,则a2015的值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校篮球队五名主力队员的身高分别是 173,180,181,176,178(单位:cm),则这五名运动员身高的中位数是( )
A. 181cm B. 180cm C. 178cm D. 176cm
相关试题

