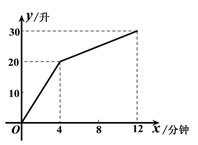
【题目】一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分钟)之间的部分关系如图象所示.求从关闭进水管起需要多少分钟该容器内的水恰好放完.
参考答案:
【答案】从关闭进水管起需要8分钟该容器内的水恰好放完.
【解析】
先根据函数图象求出进水管的进水量和出水管的出水量,由工程问题的数量关系就可以求出结论.
解:由函数图象,得:
进水管每分钟的进水量为:20÷4=5(升).
设出水管每分钟的出水量为 m升,由函数图象,得:
20+(5-m)×(12-4)=30.
解得:m=![]()
∴30÷![]() =8(分钟).
=8(分钟).
即从关闭进水管起需要8分钟该容器内的水恰好放完.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在一条直线道路上分别从相距1500米的A,B 两点同时出发,相向而行,当两人相遇后,甲继续向点B前进(甲到达点B时停止运动),乙也立即向B点返回.在整个运动过程中,甲、乙均保持匀速运动.甲、乙两人之间的距离y(米)与乙运动的时间x(秒) 之间的关系如图所示.则甲到B点时,乙距B点的距离是________米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购进商品后,都加价40%作为销售价,元旦期间搞优惠促销,决定由顾客抽奖确定折扣,某顾客购买甲、乙两种商品,分别抽到七折和九折,共付款399元,商场共盈利49元,甲、乙两种商品的进价分别为多少元?
-
科目: 来源: 题型:
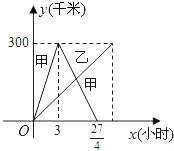
查看答案和解析>>【题目】已知:甲乙两车分别从相距300千米的A、B两地同时出发相向而行,其中甲到达B地后立即返回,如图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.
(1)求甲车离出发地的距离y甲(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量的取值范围;
(2)若已知乙车行驶的速度是40千米/小时,求出发后多长时间,两车离各自出发地的距离相等;
(3)在上述条件下,直接写出它们在行驶过程中相遇时的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(5,1). ①画出△ABC关于y轴对称的△A1B1C1 , 并写出点C1的坐标;
②连结BC1 , 在坐标平面的格点上确定一个点P,使△B C1P是以B C1为底的等腰直角三角形,画出△B C1P,并写出所有P点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图四边形ABCD是一块草坪,量得四边长AB=3m,BC=4m,DC=12m,AD=13m,∠B=90°,求这块草坪的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E、F是平行四边形ABCD对角线AC上两点,AE=CF.
证明(1)△ABE≌△CDF;
(2)BE∥DF.

相关试题

