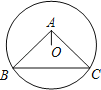
【题目】如图,⊙O过点B、C.圆心O在等腰直角△ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为 .
参考答案:
【答案】![]()
【解析】
试题分析:过O作OD⊥BC,由垂径定理可知BD=CD=![]() BC,根据△ABC是等腰直角三角形可知∠ABC=45°,故△ABD也是等腰直角三角形,BD=AD,再由OA=1可求出OD的长,在Rt△OBD中利用勾股定理即可求出OB的长.
BC,根据△ABC是等腰直角三角形可知∠ABC=45°,故△ABD也是等腰直角三角形,BD=AD,再由OA=1可求出OD的长,在Rt△OBD中利用勾股定理即可求出OB的长.
解:过O作OD⊥BC,
∵BC是⊙O的一条弦,且BC=6,
∴BD=CD=![]() BC=
BC=![]() ×6=3,
×6=3,
∴OD垂直平分BC,又AB=AC,
∴点A在BC的垂直平分线上,即A,O及D三点共线,
∵△ABC是等腰直角三角形,
∴∠ABC=45°,
∴△ABD也是等腰直角三角形,
∴AD=BD=3,
∵OA=1,
∴OD=AD﹣OA=3﹣1=2,
在Rt△OBD中,
OB=![]() =
=![]() =
=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把方程2x(x﹣3)=3x+2化成一元二次方程的一般形式后,它的一次项系数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是( )
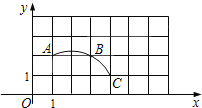
A.点(0,3) B.点(2,3) C.点(5,1) D.点(6,1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P的坐标是(2,3),则点P到x轴的距离是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+
 x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
(1)请直接写出二次函数y=ax2+
 x+c的表达式;
x+c的表达式;(2)判断△ABC的形状,并说明理由;
(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请直接写出此时点N的坐标;
(4)若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:5+3x=8+2x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】商贸大楼共有四层,第一层有商品(a+b)2种,第二层有商品a(a+b)种,第三层有商品b(a+b)种,第四层有商品(b+a)2种.若a+b=10,则这座商贸大楼共有商品多少种?
相关试题

