【题目】901班的全体同学根据自己的兴趣爱好参加了六个学生社团（每个学生必须参加且只参加一个），为了了解学生参加社团的情况，学生会对该班参加各个社团的人数进行了统计，绘制成了如图不完整的扇形统计图，已知参加“读书社”的学生有15人，请解答下列问题：

（1）该班的学生共有 名；

（2）若该班参加“吉他社”与“街舞社”的人数相同，请你计算，“吉他社”对应扇形的圆心角的度数；

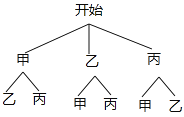
（3）901班学生甲、乙、丙是“爱心社”的优秀社员，现要从这三名学生中随机选两名学生参加“社区义工”活动，请你用画树状图或列表的方法求出恰好选中甲和乙的概率．

参考答案：

【答案】（1）60；（2）36°；（3）．

【解析】试题（1）利用参加“读书社”的学生数除以所占比例进而求出总人数；

（2）首先求出参加“吉他社”的学生在全班学生中所占比例，进而求出对应扇形的圆心角的度数；

（3）首先画出树状图，进而求出恰好选中甲和乙的概率．

试题解析：（1）∵参加“读书社”的学生有15人，且在扇形统计图中，所占比例为：25%，∴该班的学生共有：15÷25%=60（人）；故答案为：60；

（2）参加“吉他社”的学生在全班学生中所占比例为： =10%，所以，“吉他社”对应扇形的圆心角的度数为：360°×10%=36°；

（3）画树状图如下：

，

由树状图可知，共有6种可能的情况，其中恰好选中甲和乙的情况有2种，故P（选中甲和乙）==．

关闭