搜索
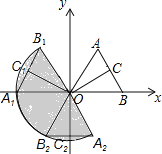
【题目】如图，△AOB是等边三角形，且B（2，0），OC是AB边的中线，将△AOB绕点O逆时针旋转120°得到△A1OB1．
（1）B1的坐标是_______（直接写出结果即可）；
（2）请画出将△A1OB1绕点O逆时针旋转120°得到的△A2OB2，并按图形旋转规律画出阴影部分；
（3）计算点B旋转到点B1所经过的弧形路线长（结果保留π）．
参考答案：
【答案】(1)（﹣1， 
）；(2) 
【解析】试题分析：（1）直接利用等边三角形的性质结合锐角三角函数关系得出B1的坐标即可；
（2）直接利用旋转的性质得出对应点位置进而得出答案；
（3）直接利用弧长公式得出答案．
试题解析：(1)∵△AOB是等边三角形,且B(2,0)，
可得
的坐标是： 
故答案为： 
(2)如图所示： 
即为所求；
(3)点B旋转到点
所经过的弧形路线长为： 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，二次函数y=-x2+ax+b的图象与x轴交于A（-
，0），B（2，0）两点，且与y轴交于点C．（1）求该抛物线的解析式，并判断△ABC的形状；
（2）设P是x轴上方的抛物线上的动点，过点P作PM⊥x轴，垂足为M，是否存在点P，使得以P、A 、M为顶点的三角形与ABC相似？若存在，求出点P的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，在□ABCD中，E，F分别在BC，AD上，若想使四边形AFCE为平行四边形，须添加一个条件，这个条件可以是（ ）
①AF=CF；②AE=CF；③∠BAE=∠FCD；④∠BEA=∠FCE。
A. ①或② B. ②或③ C. ③或④ D. ①或③或④
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，两个等腰直角三角形△ABC和△CDE中，∠ACB＝∠DCE＝90°，AB＝13
，CD＝5，△CDE绕点C在平面内自由旋转，当A、E、D三点共线时，AD的长是______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示,铅笔图案的五个顶点的坐标分别是(0,1),(4,1),(5,1.5),(4,2),(0,2).将图案向下平移2个单位长度,画出相应的图案,并写出平移后相应五个顶点的坐标.
-
科目： 来源： 题型：
查看答案和解析>>【题目】材料：帕普斯借助函数给出了一种“三等分锐角”的方法，具体如下：
①建立平面直角坐标系，将已知锐角∠AOB的顶点与原点O重合，角的一边OB与x轴正方向重合；
②在平面直角坐标系里，绘制函数y＝
的图象，图象与已知角的另一边OA交于点P；③以P为圆心，2OP为半径作弧，交函数y＝
的图象于点R；④分别过点P和R作x轴和y轴的平行线，两线相交于点M、Q；
⑤连接OM，得到∠MOB，这时∠MOB＝
∠AOB．根据以上材料解答下列问题：
（1）设点P的坐标为（a，
），点R的坐标为（b，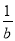
），则点M的坐标为 ；（2）求证：点Q在直线OM上；
（3）求证：∠MOB＝
∠AOB；（4）应用上述方法得到的结论，如何三等分一个钝角（用文字简要说明）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图（1），在平面直角坐标系中，等腰直角三角形AOB的斜边OB在x轴上，直线y＝2x－2经过等腰直角三角形AOB的直角顶点A，交y轴于点C．
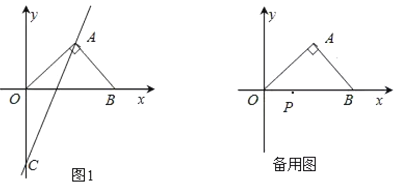
（1）点C坐标是（ ， ）；点A坐标是（ ， ）；
（2）若D是坐标平面内任意一点，使点A、C、O、D刚好能构成平行四边形，请直接写出符合条件的点D的坐标；
（3）若点P是x轴上一动点．点Q的坐标是（a，
），△PAQ是以点A为直角顶点的等腰三角形．求出a的值并写出点Q的坐标．
相关试题
