【题目】已知,如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C,A(1,﹣1),B(3,﹣1),动点P从点O出发,沿着x轴正方向以每秒2个单位长度的速度移动,过点P作PQ垂直于直线OA,垂足为点Q,设点P移动的时间t秒(0<t<2),△OPQ与四边形OABC重叠部分的面积为S.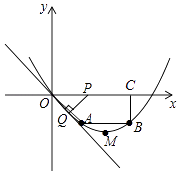
(1)求经过O、A、B三点的抛物线的解析式,并确定顶点M的坐标;
(2)用含t的代数式表示点P、点Q的坐标;
(3)求出S与t的函数关系式.
参考答案:
【答案】
(1)
解:设抛物线解析式为y=ax2+bx(a≠0),
把点A(1,﹣1),B(3,﹣1)代入得,
![]() ,
,
解得: 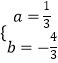 ,
,
故抛物线解析式为y= ![]() x2﹣
x2﹣ ![]() x
x
(2)
解:∵点P从点O出发速度是每秒2个单位长度,
∴OP=2t,
∴点P的坐标为(2t,0),
∵A(1,﹣1),
∴∠AOC=45°,
∴点Q到x轴、y轴的距离都是 ![]() OP=
OP= ![]() ×2t=t,
×2t=t,
∴点Q的坐标为(t,﹣t)
(3)
解:如图,点Q与点A重合时,
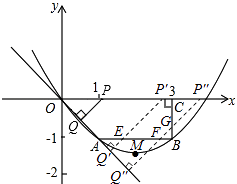
OP=1×2=2,t=2÷2=1,
点P与点C重合时,OP=3,t=3÷2=1.5,
t=2时,OP=2×2=4,PC=4﹣3=1,此时PQ经过点B,
所以,分三种情况讨论:
①0<t≤1时,重叠部分的面积等于△POQ的面积,S= ![]() ×(2t)×
×(2t)× ![]() =t2,
=t2,
②1<t≤1.5时,重叠部分的面积等于两个等腰直角三角形的面积的差,
S=S△OP′Q′﹣S△AEQ′= ![]() ×(2t)×
×(2t)× ![]() ﹣
﹣ ![]() ×(
×( ![]() t﹣
t﹣ ![]() )2=2t﹣1;
)2=2t﹣1;
③1.5<t<2时,重叠部分的面积等于梯形的面积减去一个等腰直角三角形的面积
S=S梯形OABC﹣S△BGF= ![]() ×(2+3)×1﹣
×(2+3)×1﹣ ![]() ×[1﹣(2t﹣3)]2=﹣2(t﹣2)2+
×[1﹣(2t﹣3)]2=﹣2(t﹣2)2+ ![]() ;
;
所以,S与t的关系式为S=  .
.
【解析】(1)设抛物线解析式为y=ax2+bx(a≠0),然后把点A、B的坐标代入求出a、b的值,即可得解,再把函数解析式整理成顶点式形式,然后写出顶点M的坐标;(2)根据点P的速度求出OP,即可得到点P的坐标,再根据点A的坐标求出∠AOC=45°,然后判断出△POQ是等腰直角三角形,根据等腰直角三角形的性质求出点Q的坐标即可;(3)求出点Q与点A重合时的t=1,点P与点C重合时的t=1.5,t=2时PQ经过点B,然后分①0<t≤1时,重叠部分的面积等于△POQ的面积,②1<t≤1.5时,重叠部分的面积等于两个等腰直角三角形的面积的差,③1.5<t<2时,重叠部分的面积等于梯形的面积减去一个等腰直角三角形的面积分别列式整理即可得解.
【考点精析】利用二次函数的性质对题目进行判断即可得到答案,需要熟知增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.
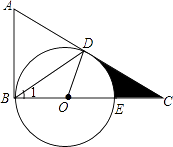
(1)求证:AC是⊙O的切线;
(2)若∠A=60°,⊙O的半径为2,求阴影部分的面积.(结果保留根号和π) -
科目: 来源: 题型:
查看答案和解析>>【题目】为了能以“更新、更绿、更洁、更宁”的城市形象迎接2011年大运会的召开,深圳市全面实施市容市貌环境提升行动.某工程队承担了一段长为1500米的道路绿化工程,施工时有两张绿化方案: 甲方案是绿化1米的道路需要A型花2枝和B型花3枝,成本是22元;
乙方案是绿化1米的道路需要A型花1枝和B型花5枝,成本是25元.
现要求按照乙方案绿化道路的总长度不能少于按甲方案绿化道路的总长度的2倍.
(1)求A型花和B型花每枝的成本分别是多少元?
(2)求当按甲方案绿化的道路总长度为多少米时,所需工程的总成本最少?总成本最少是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知OA⊥OB,OA=4,OB=3,以AB为边作矩形ABCD,使AD=a,过点D作DE垂直OA的延长线交于点E.
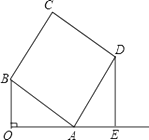
(1)证明:△OAB∽△EDA;
(2)当a为何值时,△OAB与△EDA全等?请说明理由,并求出此时点C到OE的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,B,C两点把线段AD分成2:5:3三部分,M为AD的中点,BM=6cm,求CM和AD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】商场打折前,买1件A商品和1件B商品用了20元,买30件A商品和40件B商品用了680元.打折后,买100件A商品100件B商品用了1800元.请根据上述信息解决下列问题:
(1)打折前A、B两种商品的单价分别是多少?
(2)请在(1)的基础上提出一个能使题目剩余条件解决的问题,并加以解决.
-
科目: 来源: 题型:
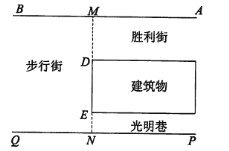
查看答案和解析>>【题目】如图所示,一段街道的两边缘所在直线分别为AB, PQ,并且AB∥PQ.建筑物的一端DE所在的直线MN⊥AB于点M,交PQ于点N,步行街宽MN为13.4米,建筑物宽DE为6米,光明巷宽EN为2.4米.小亮在胜利街的A处,测得此时AM为12米,求此时小亮距建筑物拐角D处有多远?
相关试题

