【题目】如图,AB是⊙O的直径,点C在⊙O上,连接AC,BC,点D是BA延长线上一点,且AC=AD,若∠B=30°,AB=2,则CD的长是( )
A.![]()
B.2
C.1
D.![]()
参考答案:
【答案】D
【解析】解:连接OC,
∵AB是⊙O的直径,
∴∠ACB=90°.
∵∠B=30°,
∴∠BAC=60°.
∵AC=AD,
∴∠D=∠ACD=30°.
∵OC=OB,∠B=30°,
∴∠DOC=60°,
∴∠OCD=90°.
∵AB=2,
∴OC=1,
∴CD= ![]() =
= ![]() =
= ![]() .
.
故选D.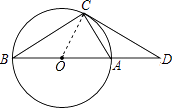
【考点精析】通过灵活运用圆周角定理,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,对角线AC , BD相交于点O , 且AC=6cm,BD=8cm,动点P , Q分别从点B , D同时出发,运动速度均为1cm/s,点P沿B→C→D运动,到点D停止,点Q沿D→O→B运动,到点O停止1s后继续运动,到点B停止,连接AP , AQ , PQ . 设△APQ的面积为y(cm2)(这里规定:线段是面积0的几何图形),点P的运动时间为x(s).

(1)填空:AB=cm,AB与CD之间的距离为cm;
(2)当4≤x≤10时,求y与x之间的函数解析式;
(3)直接写出在整个运动过程中,使PQ与菱形ABCD一边平行的所有x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,将△ABC绕着点A逆时针旋转得到△ADE,点C落在边AD上,连接BD.若∠DAE=α,则用含α的式子表示∠CBD的大小是( )

A.α
B.90°﹣α
C.
D.

-
科目: 来源: 题型:
查看答案和解析>>【题目】以正方形ABCD的边AD作等边△ADE,则∠BEC的度数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC是正方形ABCD的对角线,将△ACD绕着点A顺时针旋转后得到△AC′D′,点D′落在AC上,C′D′交BC于点E,若AB=1,则图中阴影部分图形的面积是 .
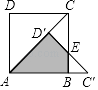
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,E是BC上的一点,连接AE,过B点作BH⊥AE,垂足为点H,延长BH交CD于点F,连接AF.
(1)求证AE=BF;
(2)若正方形的边长是5,BE=2,求AF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴是x=1,有以下四个结论:
①abc>0;②b2﹣4ac>0;③b=﹣2a;④a+b+c>2,
其中正确的是(填写序号)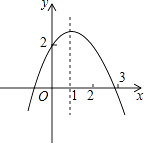
相关试题

