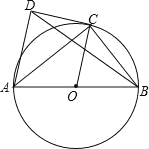
【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.
(1)求证:AC平分∠DAB;
(2)若sin∠ABC=![]() ,求tan∠BDC的值.
,求tan∠BDC的值.
参考答案:
【答案】(1)证明见解析;
(2)tan∠CDB=tan∠DBM=![]() =
=![]() =
=![]() .
.
【解析】
试题分析:(1)先证明AD∥OC,得∠DAC=∠ACO,再根据OA=OC得∠OAC=∠OCA,由此即可证明.
(2)连接BM、OC交于点N,根据sin∠ABC=sin∠BCN=![]() =
=![]() ,设BN=4k,BC=5k,则CN=3k,求出DM,BM,根据tan∠CDB=tan∠DBM=
,设BN=4k,BC=5k,则CN=3k,求出DM,BM,根据tan∠CDB=tan∠DBM=![]() 即可解决问题.
即可解决问题.
试题解析:(1)∵DC是⊙O切线,
∴OC⊥CD,∵AD⊥CD,
∴AD∥CO,
∴∠DAC=∠ACO,
∵OA=OC,
∴∠OAC=∠ACO,
∴∠DAC=∠CAO,
∴AC平分∠DAB.
(2)连接BM、OC交于点N.
∵AB是直径,
∴∠AMB=90°,∵AD∥OC,
∴∠ONB=∠AMB=90°=∠CNB,
∵OC=OB,
∴∠OCB=∠OBC,
∴sin∠ABC=sin∠BCN=![]() =
=![]() ,设BN=4k,BC=5k,则CN=3k,
,设BN=4k,BC=5k,则CN=3k,
∵∠CDM=∠DMN=∠DCN=90°,
∴四边形DMNC是矩形,
∴DM=CN=3k,MN=BN=4k,CD∥BM,
∴∠CDB=∠DBM,
∴tan∠CDB=tan∠DBM=![]() =
=![]() =
=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校计划用104 000元购置一批电脑(这批款项须恰好用完,不得剩余或追加).经过招标,其中平板电脑每台1600元,台式电脑每台4000元,笔记本电脑每台4600元.
(1)若学校同时购进其中两种不同类型的电脑共50台,请你帮学校设计该如何购买;
(2)若学校同时购进三种不同类型的电脑共26台(三种类型的电脑都有),并且要求笔记本电脑的购买量不少于15台. -
科目: 来源: 题型:
查看答案和解析>>【题目】A,B两地相距80km,甲、乙两人沿同一条路从A地到B地.l1,l2分别表示甲、乙两人离开A地的距离s(km)与时间t(h)之间的关系.
(1) 乙先出发________h后,甲才出发;
(2) 请分别求出甲、乙的速度;并直接写出l1、、l2的表达式.
(3) 甲到达B地时,乙距B地还有多远?,乙还需几小时到达B地?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在弹性限度内,弹簧的长度y(cm)是所挂物体质量X(kg)的一次函数.某弹簧不挂物体时,长14.5cm;当所挂物体的质量为3kg时,弹簧长16cm.
(1)写出y与x之间的关系式;
(2)并求当所挂物体的质量为4kg时弹簧的长度.
-
科目: 来源: 题型:
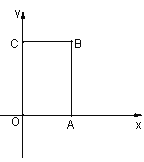
查看答案和解析>>【题目】如图,在长方形OABC中,O为平面直角坐标系的原点,OA=4,AB=6,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的线路移动.
(1)点B的坐标为 ;
(2)当点P移动4秒时,请指出点P的位置,并求出点P的坐标.
-
科目: 来源: 题型:
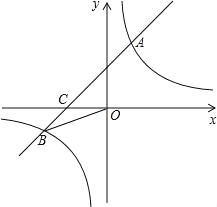
查看答案和解析>>【题目】已知:如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数
 的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,﹣2),tan∠BOC=
的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,﹣2),tan∠BOC= .
.(1)求该反比例函数和一次函数的解析式;
(2)在x轴上有一点E(O点除外),使得△BCE与△BCO的面积相等,求出点E的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.
(1)如果△ABC三个顶点的坐标分别是A(﹣2,0),B(﹣1,0),C(﹣1,2),△ABC关于y轴的对称图形是△A1B1C1,△A1B1C1关于直线l的对称图形是△A2B2C2,写出△A2B2C2的三个顶点的坐标;
(2)如果点P的坐标是(﹣a,0),其中0<a<3,点P关于y轴的对称点是P1,点P1关于直线l的对称点是P2,求PP2的长.


备用图
相关试题

