【题目】如图,已知∠AOB=120°,射线OA绕点O以每秒钟6°的速度逆时针旋转到OP,设射线OA旋转OP所用时间为t秒(t<30). 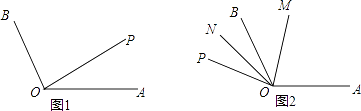
(1)如图1,直接写出∠BOP=°(用含t的式子表示);
(2)若OM平分∠AOP,ON平分∠BOP. ①当OA旋转到如图1所示OP处,请完成作图并求∠MON的度数;
②当OA旋转到如图2所示OP处,若2∠BOM=3∠BON,求t的值.
参考答案:
【答案】
(1)(120﹣6t)
(2)解:∵OM平分∠AOP,ON平分∠BOP,
∴∠MOP= ![]() ∠AOP=3t,∠NOP=
∠AOP=3t,∠NOP= ![]() ∠BOP=60﹣3t,
∠BOP=60﹣3t,
∴∠MON=∠MOP+∠NOP=3t+60﹣3t=60°;
∵OM平分∠AOP,ON平分∠BOP,
∴∠MOA=∠MOP= ![]() ∠AOP=3t,
∠AOP=3t,
∠BON=∠NOP= ![]() ∠BOP=3t﹣60,
∠BOP=3t﹣60,
∵2∠BOM=3∠BON,
即2(120﹣3t)=3(3t﹣60),
解得t=28.
【解析】解:(1)∵∠AOB=120°,∠AOP=6t, ∴∠BOP=(120﹣6t)°.
故答案为:(120﹣6t);
(1)由于∠AOB=120°,∠AOP=6t,即可得到∠BOP=(120﹣6t)°;(2)根据角平分线的定义得到∠MOP= ![]() ∠AOP=3t,∠NOP=
∠AOP=3t,∠NOP= ![]() ∠BOP=60﹣3t,根据线段的和差即可得到结论;(3)根据角平分线的定义得到∠MOA=∠MOP=
∠BOP=60﹣3t,根据线段的和差即可得到结论;(3)根据角平分线的定义得到∠MOA=∠MOP= ![]() ∠AOP=3t,∠BON=∠NOP=
∠AOP=3t,∠BON=∠NOP= ![]() ∠BOP=3t﹣60,根据已知条件列方程即可得到结论.
∠BOP=3t﹣60,根据已知条件列方程即可得到结论.
-
科目: 来源: 题型:
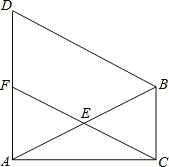
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形,E是AB的中点,连接CE并延长交AD于F.求证:
(1)△AEF≌△BEC;
(2)四边形BCFD是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的方程x2+4x+2m=0有实数根.
(1)求m的取值范围;
(2)若m为正整数,且该方程的根都是整数,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地连续九天的最高气温统计如下表:
最高气温(℃)
22
23
24
25
天数
1
2
2
4
则这组数据的中位数与众数分别是( )
A. 24,25 B. 24.5,25 C. 25,24 D. 23.5,24
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,顶点D与边AB的中点重合.
(1)若DE经过点C,DF交AC于点G,求证:∠AGD=90°
(2)求图1中重叠部分(△DCG)的面积;
(3)合作交流:“希望”小组受问题(1)(2)的启发,将△DEF绕点D旋转,使DE⊥AB交AC于点H,DF交AC于点G,如图2,求重叠部分(△DGH)的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】当五个整数从小到大排列后,其中位数是4,如果这组数据的唯一众数是6,那么这组数据可能的最大的和是_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简再求值
(1)﹣9y+6x2+3(y﹣ x2),其中x=2,y=﹣1.
x2),其中x=2,y=﹣1.
(2)2a2b﹣[2a2+2(a2b+2a2)],其中a= ,b=1.
,b=1.
相关试题

