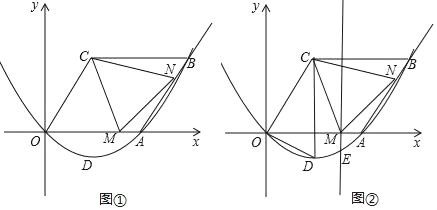
【题目】如图抛物线y=ax2+bx,过点A(4,0)和点B(6,2![]() ),四边形OCBA是平行四边形,点M(t,0)为x轴正半轴上的点,点N为射线AB上的点,且AN=OM,点D为抛物线的顶点.
),四边形OCBA是平行四边形,点M(t,0)为x轴正半轴上的点,点N为射线AB上的点,且AN=OM,点D为抛物线的顶点.
(1)求抛物线的解析式,并直接写出点D的坐标;
(2)当△AMN的周长最小时,求t的值;
(3)如图②,过点M作ME⊥x轴,交抛物线y=ax2+bx于点E,连接EM,AE,当△AME与△DOC相似时.请直接写出所有符合条件的点M坐标.
参考答案:
【答案】(1)y=![]() x2﹣
x2﹣![]() x,点D的坐标为(2,﹣
x,点D的坐标为(2,﹣![]() );(2)t=2;(3)M点的坐标为(2,0)或(6,0).
);(2)t=2;(3)M点的坐标为(2,0)或(6,0).
【解析】
(1)利用待定系数法求抛物线解析式;利用配方法把一般式化为顶点式得到点D的坐标;
(2)连接AC,如图①,先计算出AB=4,则判断平行四边形OCBA为菱形,再证明△AOC和△ACB都是等边三角形,接着证明△OCM≌△ACN得到CM=CN,∠OCM=∠ACN,则判断△CMN为等边三角形得到MN=CM,于是△AMN的周长=OA+CM,由于CM⊥OA时,CM的值最小,△AMN的周长最小,从而得到t的值;
(3)先利用勾股定理的逆定理证明△OCD为直角三角形,∠COD=90°,设M(t,0),则E(t,![]() t2-
t2-![]() t),根据相似三角形的判定方法,当
t),根据相似三角形的判定方法,当![]() 时,△AME∽△COD,即|t-4|:4=|
时,△AME∽△COD,即|t-4|:4=|![]() t2-
t2-![]() t |:
t |:![]() ,当
,当![]() 时,△AME∽△DOC,即|t-4|:
时,△AME∽△DOC,即|t-4|:![]() =|
=|![]() t2-
t2-![]() t |:4,然后分别解绝对值方程可得到对应的M点的坐标.
t |:4,然后分别解绝对值方程可得到对应的M点的坐标.
(1)把A(4,0)和B(6,2![]() )代入y=ax2+bx得
)代入y=ax2+bx得
![]() ,解得
,解得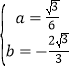 ,
,
∴抛物线解析式为y=![]() x2-
x2-![]() x;
x;
∵y=![]() x2-
x2-![]() x =
x =![]() -2) 2-
-2) 2-![]() ;
;
∴点D的坐标为(2,-![]() );
);
(2)连接AC,如图①,

AB=![]() =4,
=4,
而OA=4,
∴平行四边形OCBA为菱形,
∴OC=BC=4,
∴C(2,2![]() ),
),
∴AC=![]() =4,
=4,
∴OC=OA=AC=AB=BC,
∴△AOC和△ACB都是等边三角形,
∴∠AOC=∠COB=∠OCA=60°,
而OC=AC,OM=AN,
∴△OCM≌△ACN,
∴CM=CN,∠OCM=∠ACN,
∵∠OCM+∠ACM=60°,
∴∠ACN+∠ACM=60°,
∴△CMN为等边三角形,
∴MN=CM,
∴△AMN的周长=AM+AN+MN=OM+AM+MN=OA+CM=4+CM,
当CM⊥OA时,CM的值最小,△AMN的周长最小,此时OM=2,
∴t=2;
(3)∵C(2,2![]() ),D(2,-
),D(2,-![]() ),
),
∴CD=![]() ,
,
∵OD=![]() ,OC=4,
,OC=4,
∴OD2+OC2=CD2,
∴△OCD为直角三角形,∠COD=90°,
设M(t,0),则E(t,![]() t2-
t2-![]() t),
t),
∵∠AME=∠COD,
∴当![]() 时,△AME∽△COD,即|t-4|:4=|
时,△AME∽△COD,即|t-4|:4=|![]() t2-
t2-![]() t |:
t |:![]() ,
,
整理得|![]() t2-
t2-![]() t|=
t|=![]() |t-4|,
|t-4|,
解方程![]() t2-
t2-![]() t =
t =![]() (t-4)得t1=4(舍去),t2=2,此时M点坐标为(2,0);
(t-4)得t1=4(舍去),t2=2,此时M点坐标为(2,0);
解方程![]() t2-
t2-![]() t =-
t =-![]() (t-4)得t1=4(舍去),t2=-2(舍去);
(t-4)得t1=4(舍去),t2=-2(舍去);
当![]() 时,△AME∽△DOC,即|t-4|:
时,△AME∽△DOC,即|t-4|:![]() =|
=|![]() t2-
t2-![]() t |:4,整理得|
t |:4,整理得|![]() t2-
t2-![]() t |=|t-4|,
t |=|t-4|,
解方程![]() t2-
t2-![]() t =t-4得t1=4(舍去),t2=6,此时M点坐标为(6,0);
t =t-4得t1=4(舍去),t2=6,此时M点坐标为(6,0);
解方程![]() t2-
t2-![]() t =-(t-4)得t1=4(舍去),t2=-6(舍去);
t =-(t-4)得t1=4(舍去),t2=-6(舍去);
综上所述,M点的坐标为(2,0)或(6,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年女排世界杯中,中国女排以11站全胜且只丢3局的成绩成功卫冕本届世界杯冠军.某校七年级为了弘扬女排精神,组建了排球社团,通过测量同学们的身高(单位:cm),并绘制了如下两幅不完整的统计图,请结合图中提供的信息,解答下列问题.

(1)填空:样本容量为___,a=___;
(2)把频数分布直方图补充完整;
(3)若从该组随机抽取1名学生,估计这名学生身高低于165cm的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司销售A,B两种品牌的教学设备,这两种教学设备的进价和售价如表所示
A
B
进价(万元/套)
1.5
1.2
售价(万元/套)
1.8
1.4
该公司计划购进两种教学设备若干套,共需66万元,全部销售后可获毛利润12万元.
(1)该公司计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该公司决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少的数量的1.5倍.若用于购进这两种教学设备的总资金不超过68万元,问A种设备购进数量至多减少多少套?
-
科目: 来源: 题型:
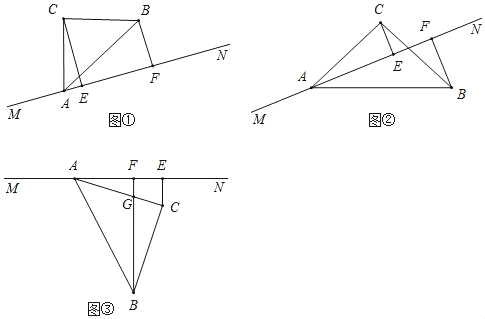
查看答案和解析>>【题目】如图,在等腰直角△ABC中,∠C是直角,点A在直线MN上,过点C作CE⊥MN于点E,过点B作BF⊥MN于点F.
(1)如图1,当C,B两点均在直线MN的上方时,
①直接写出线段AE,BF与CE的数量关系.
②猜测线段AF,BF与CE的数量关系,不必写出证明过程.
(2)将等腰直角△ABC绕着点A顺时针旋转至图2位置时,线段AF,BF与CE又有怎样的数量关系,请写出你的猜想,并写出证明过程.
(3)将等腰直角△ABC绕着点A继续旋转至图3位置时,BF与AC交于点G,若AF=3,BF=7,直接写出FG的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘轮船在A处测得灯塔P位于其东北方向上,轮船沿正东方向航行30海里到达B处后,此时测得灯塔P位于其北偏东30°方向上,此时轮船与灯塔P的距离是( )海里.

A. 15
 +15 B. 30
+15 B. 30 +30 C. 45+15
+30 C. 45+15 D. 60
D. 60 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个图案中,是轴对称图形的是( )
A.
 B.
B.
C.
 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形都是由两样大小的小圆圈按一定规律组成的,其中第①个图形中一共有7个小圆圈,第②个图形中一共有13个小圆圈,第③个图形中一共有21个小圆圈,…,按此规律排列,则第⑧个图形中小圆圈的个数为( )

A. 68 B. 88 C. 91 D. 93
相关试题

