【题目】已知,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=40°,试探究线段BD与CE的数量关系与直线BD与CE相交构成的锐角的度数.


(1)如图①,当点D,E分别在△ABC的边AB,AC上时,BD与CE的数量关系是___________,直线BD与CE相交构成的锐角的度数是_____________.
(2)将图①中△DAE绕点A逆时针旋转一个角度到图②的位置,则(1)中的两个结论是否仍然成立?说明理由.
(3)将图②中△DAE继续绕点A按逆时针方向继续旋转到点D落在CA的延长线时,请画出图形,并直接写出(1)中的两个结论是否仍然成立.
参考答案:
【答案】(1)BD=CE;40°;(2)仍然成立;理由见解析;(3)成立;图形见解析.
【解析】
(1)根据图形和已知条件即可得出结论;
(2)延长BD、CE,相交于点F,由∠BAC=∠DAE得出∠DAB=∠EAC,利用SAS证得△DAB≌△EAC,根据全等三角形的性质得到BD=CE,∠DBA=∠ECA,根据三角形内角和定理得出∠ABC+∠ACB=140°即∠ABC+∠BCF+∠ECA=140°,利用等量代换得到∠ABC+∠BCF+∠DBA=140°,最后利用三角形内角和定理即可得出结论;
(3)方法同(2).
(1)BD=CE;40°;
如图①∵AB=AC,AD=AE
∴AB-AD=AC-AE
∴BD=CE
直线BD与CE相交构成的锐角是∠A,
∴∠A=∠BAC=∠DAE=40°
故答案为:BD=CE;40°;
(2)仍然成立
证明:延长BD、CE,相交于点F,如图所示

∵∠BAC=∠DAE=40°
∴∠BAC﹣∠BAE=∠DAE﹣∠BAE
即∠DAB=∠EAC
又∵AB=AC,AD=AE,
∴△DAB≌△EAC(SAS)
∴BD=CE,∠DBA=∠ECA
∵∠BAC=40°,∠BAC+∠ABC+∠ACB=180°
∴∠ABC+∠ACB=140°
∴∠ABC+∠BCF+∠ECA=140°
∴∠ABC+∠BCF+∠DBA=140°即∠FCB+∠FBC=140°
∵∠FCB+∠FBC+∠F=180°
∴∠F=40°
(3)(1)中结论仍然成立,如图所示

证明:∵∠BAC=∠DAE=40°
∴∠BAC+∠BAE=∠DAE+∠BAE
即∠DAB=∠EAC
又∵AB=AC,AD=AE,
∴△DAB≌△EAC(SAS)
∴BD=CE,∠DBA=∠ECA
∵∠BAC=40°,∠BAC+∠ABC+∠ACB=180°
∴∠ABC+∠ACB=140°
∴∠ABC+∠BCF+∠FCA=140°
∴∠ABC+∠BCF+∠DBA=140°,即∠FCB+∠FBC=140°
∵∠FCB+∠FBC+∠BFC=180°
∴∠BFC=40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织一项公益知识竞赛,比赛规定:每个班级由2名男生、2名女生及1名班主任老师组成代表队.但参赛时,每班只能有3名队员上场参赛,班主任老师必须参加,另外2名队员分别在2名男生和2名女生中各随机抽出1名.初三(1)班由甲、乙2名男生和丙、丁2名女生及1名班主任组成了代表队,求恰好抽到由男生甲、女生丙和这位班主任一起上场参赛的概率.(请用“画树状图”或“列表”或“列举”等方法给出分析过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在解方程x2﹣
 x+1=0的时候,奇奇的方法别出心裁:
x+1=0的时候,奇奇的方法别出心裁:解:移项得:x2+1=
 x,变形得:x2+1=
x,变形得:x2+1= x=(
x=(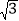 +
+ )x①,由于原方程中x≠0,故可以在①的两边同时除以x得:x+
)x①,由于原方程中x≠0,故可以在①的两边同时除以x得:x+ =
=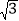 +
+ 解得:x1=
解得:x1=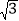 ,x2=
,x2=
这是利用对称式的典型范例,下面的问题需要你来完成:
(1)直接写出方程x﹣
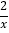 =b﹣
=b﹣ 的解:
的解:(2)由(1)的结论解关于x的方程:x﹣
 =a﹣
=a﹣ (a≠2)
(a≠2)(3)模仿奇奇的解法,解方程:x2﹣
 x+4=0.
x+4=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】暑假期间,两位家长计划带领若干名学生去旅游,他们联系了报价均为每人400元的两家旅行社.经协商,甲旅行社的优惠条件是:两位家长全额收费,学生都按七折收费;乙旅行社的优惠条件是:家长、学生都按八折收费假设这两位家长带领x名学生去旅游.
(1)如果设选择甲旅行社所用的费用为
 元,选择乙旅行社所用的费用为
元,选择乙旅行社所用的费用为 元.请写出
元.请写出 、
、 与x的关系式.
与x的关系式.(2)在(1)的前提下,请你帮助两位家长根据所带学生人数,选择哪家旅行社合算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校九年级学生的理化实验操作情况,随机抽查了40名同学实验操作的得分.根据获取的样本数据,制作了如下的条形统计图和扇形统计图.请根据相关信息,解答下列问题:

(Ⅰ)扇形 ①的圆心角的大小是 ;
(Ⅱ)求这40个样本数据的平均数、众数、中位数;
(Ⅲ)若该校九年级共有320名学生,估计该校理化实验操作得满分(10分)有多少人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与实践:
问题情境:
在数学综合与实践课上,张老师启示大家利用直线、线段以及点的运动变换进行探究活动.变换条件如下:如图 1,直线 AB,AC,BC 两两相交于 A,B,C 三点,得知△ABC是等边三角形,点 E 是直线 AC 上一动点(点 E 不与点 A,C 重合),点 F 在直线 BC上,连接 BE,EF,使 EF=BE.


独立思考:
(1)张老师首先提出了这样一个问题:如图 1,当E是线段 AC 的中点时,确定线段 AE与 CF 的数量关系,请你直接写出结论:AE____ CF(填“>” “<”或“=”).
提出问题:
(2)“奋斗”小组受此问题的启发,提出问题:若点E是线段 AC 上的任意一点,其他条件不变,(1)中的结论是否成立?该小组认为结论仍然成立,理由如下:如图 2,过点 E作 ED∥BC,交 AB 于点 D. (请你补充完整证明过程)
拓展延伸:
(3)“缜密”小组提出的问题是:动点E的运动位置如图3,图4所示,其他条件不变,根据题意补全图形,并判断线段AE与CF的数量关系是否发生变化? 请你选择其中一种予以证明.


(4)“爱心”小组提出的问题是:若等边△ABC 的边长为
 ,AE=1,则BF 的长为__________.(请你直接写出结果).
,AE=1,则BF 的长为__________.(请你直接写出结果). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC的周长为21,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )

A. 13 B. 14 C. 15 D. 16
相关试题

