Question

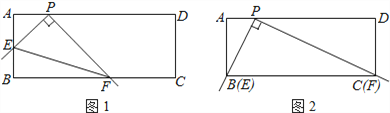
【题目】在矩形ABCD中，点P在AD上，AB=2，AP=1．将直角尺的顶点放在P处，直角尺的两边分别交AB，BC于点E，F，连接EF（如图①）．

（1）当点E与点B重合时，点F恰好与点C重合（如图②），求PC的长；

（2）探究：将直尺从图②中的位置开始，绕点P顺时针旋转，当点E和点A重合时停止．在这个过程中，请你观察、猜想，并解答：

①tan∠ PEF的值是否发生变化？请说明理由；

②直接写出从开始到停止，线段EF的中点经过的路线长．

Answer 1

【答案】（1）PC=2；（2）①∠PEF的大小不变．②

【解析】试题分析：（1）由勾股定理求PB，利用互余关系证明△APB∽△DCP，利用相似比求PC；

（2）①tan∠PEF的值不变．过F作FG⊥AD，垂足为G，同（1）的方法证明△APB∽△DCP，得相似比=2，再利用锐角三角函数的定义求值；

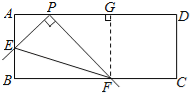
②如图3，画出起始位置和终点位置时，线段EF的中点O1，O2，连接O1O2，线段O1O2即为线段EF的中点经过的路线长，也就是△BPC的中位线．

试题解析：（1）在矩形ABCD中，∠A=∠D=90°，

AP=1，CD=AB=2，则PB=，

∴∠ABP+∠APB=90°，

又∵∠BPC=90°，

∴∠APB+∠DPC=90°，

∴∠ABP=∠DPC，

∴△APB∽△DCP，

∴，即，

∴PC=2；

（2）①tan∠PEF的值不变．

理由：过F作FG⊥AD，垂足为G，

则四边形ABFG是矩形，

∴∠A=∠PGF=90°，GF=AB=2，

∴∠AEP+∠APE=90°，

又∵∠EPF=90°，

∴∠APE+∠GPF=90°，

∴∠AEP=∠GPF，

∴△APE∽△GPF，

∴=2，

∴Rt△EPF中，tan∠PEF==2，

∴tan∠PEF的值不变；

②设线段EF的中点为O，连接OP，OB，

∵在Rt△EPF中，OP=EF，

在Rt△EBF中，OB=EF，

∴OP=OB=EF，

∴O点在线段BP的垂直平分线上，

∴线段EF的中点经过的路线长为O1O2=PC=．