【题目】如图,直线y1=﹣ ![]() x+2与x轴,y轴分别交于B,C,抛物线y=ax2+bx+c(a≠0)经过点A,B,C,点A坐标为(﹣1,0).
x+2与x轴,y轴分别交于B,C,抛物线y=ax2+bx+c(a≠0)经过点A,B,C,点A坐标为(﹣1,0).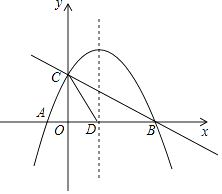
(1)求抛物线的解析式;
(2)抛物线的对称轴与x轴交于点D,连接CD,点P是直线BC上方抛物线上的一动点(不与B,C重合),当点P运动到何处时,四边形PCDB的面积最大?求出此时四边形PCDB面积的最大值和点P坐标;
(3)在抛物线上的对称轴上:是否存在一点M,使|MA﹣MC|的值最大;是否存在一点N,使△NCD是以CD为腰的等腰三角形?若存在,直接写出点M,点N的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)解:令x=0,可得y=2,令y=0,可得x=4,即点B(4,0),C(0,2);
设二次函数的解析式为y=ax2+bx+c,将点A、B、C的坐标代入解析式得,
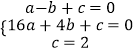 ,解得:
,解得: 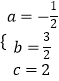 ,
,
∴二次函数的关系式为y=﹣ ![]() x2+
x2+ ![]() x+2
x+2
(2)解:如图1,过点P作PN⊥x轴于点N,交BC于点M,过点C作CE⊥PN于E,
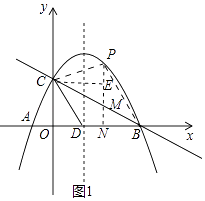
设M(a,﹣ ![]() a+2),P(a,﹣
a+2),P(a,﹣ ![]() a2+
a2+ ![]() a+2),
a+2),
∴PM=﹣ ![]() a2+
a2+ ![]() a+2﹣(﹣
a+2﹣(﹣ ![]() a+2)=﹣
a+2)=﹣ ![]() a2+2a(0≤x≤4).
a2+2a(0≤x≤4).
∵y=﹣ ![]() x2+
x2+ ![]() x+2=﹣
x+2=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,
,
∴点D的坐标为:( ![]() ,0),
,0),
∵S四边形PCDB=S△BCD+S△CPM+S△PMB= ![]() BDOC+
BDOC+ ![]() PMCE+
PMCE+ ![]() PMBN,
PMBN,
= ![]() +
+ ![]() a(﹣
a(﹣ ![]() a2+2a)+
a2+2a)+ ![]() (4﹣a)(﹣
(4﹣a)(﹣ ![]() a2+2a),
a2+2a),
=﹣a2+4a+ ![]() (0≤x≤4).
(0≤x≤4).
=﹣(a﹣2)2+ ![]() ,
,
∴a=2时,S四边形PCDB的面积最大= ![]() ,
,
∴﹣ ![]() a2+
a2+ ![]() a+2=﹣
a+2=﹣ ![]() ×22+
×22+ ![]() ×2+2=3,
×2+2=3,
∴点P坐标为:(2,3),
∴当点P运动到(2,3)时,四边形PCDB的面积最大,最大值为 ![]()
(3)解:如图2中,
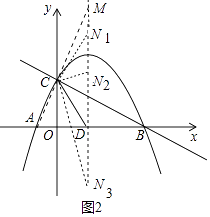
∵A(﹣1,0),C(0,2),
∴直线AC的解析式为y=2x+2,直线AC与对称轴的交点即为点M,此时|MA﹣MC|的值最大,
∴M( ![]() ,5).
,5).
∵抛物线的对称轴是x= ![]() ,
,
∴OD= ![]() ,
,
∵C(0,2),
∴OC=2.在Rt△OCD中,由勾股定理,得CD= ![]() =
= ![]() ,
,
∵△CDN是以CD为腰的等腰三角形,
∴CN1=DN2=DN3=CD.
如图2所示,作CE⊥对称轴于E,
∴EN1=ED=2,
∴DN1=4.
∴N1( ![]() ,4),N2(
,4),N2( ![]() ,
, ![]() ),N3(
),N3( ![]() ,﹣
,﹣ ![]() ).
).
【解析】(1)根据x轴上点的坐标是(x,0),y轴点的坐标是(0,y),直线y1=﹣![]() x+2与x轴,y轴分别交于B,C,得到点B(4,0)、C(0,2),由抛物线y=ax2+bx+c(a≠0)经过点A,B,C,点A坐标为(﹣1,0),用待定系数法求出抛物线的解析式;(2)由抛物线的对称轴与x轴交于点D,得到点D的坐标(
x+2与x轴,y轴分别交于B,C,得到点B(4,0)、C(0,2),由抛物线y=ax2+bx+c(a≠0)经过点A,B,C,点A坐标为(﹣1,0),用待定系数法求出抛物线的解析式;(2)由抛物线的对称轴与x轴交于点D,得到点D的坐标( ![]() ,0),由S四边形PCDB=S△BCD+S△CPM+S△PMB ,得到点P坐标(2,3),所以当点P运动到(2,3)时,四边形PCDB的面积最大,最大值为
,0),由S四边形PCDB=S△BCD+S△CPM+S△PMB ,得到点P坐标(2,3),所以当点P运动到(2,3)时,四边形PCDB的面积最大,最大值为 ![]() ;(3)由A(﹣1,0),C(0,2),代入得到直线AC的解析式为y=2x+2,直线AC与对称轴的交点即为点M,此时|MA﹣MC|的值最大,得到M(
;(3)由A(﹣1,0),C(0,2),代入得到直线AC的解析式为y=2x+2,直线AC与对称轴的交点即为点M,此时|MA﹣MC|的值最大,得到M(![]() ,5),抛物线的对称轴是x=
,5),抛物线的对称轴是x=![]() ,得到OD=
,得到OD= ![]() ,由C(0,2),得到OC=2;在Rt△OCD中,由勾股定理,得CD=
,由C(0,2),得到OC=2;在Rt△OCD中,由勾股定理,得CD=![]() ,由△CDN是以CD为腰的等腰三角形,得到CN1=DN2=DN3=CD,如图2所示,作CE⊥对称轴于E,得到EN1=ED=2,DN1=4,所以N1(
,由△CDN是以CD为腰的等腰三角形,得到CN1=DN2=DN3=CD,如图2所示,作CE⊥对称轴于E,得到EN1=ED=2,DN1=4,所以N1(![]() ,4),N2(
,4),N2(![]() ,
,![]() ),N3(
),N3( ![]() ,﹣
,﹣![]() );此题是综合题,难度较大,计算和解方程时需认真仔细.
);此题是综合题,难度较大,计算和解方程时需认真仔细.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】两块等腰直角三角形纸片AOB和COD按图1所示放置,直角顶点重合在点O处,AB=25,CD=17.保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°<α<90°)角度,如图2所示.
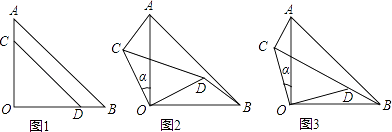
(1)利用图2证明AC=BD且AC⊥BD;
(2)当BD与CD在同一直线上(如图3)时,求AC的长和α的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=
 c,这时我们把关于x的形如ax+
c,这时我们把关于x的形如ax+ cx+b=0的一元二次方程称为“勾系一元二次方程”.
cx+b=0的一元二次方程称为“勾系一元二次方程”.
请解决下列问题:
写出一个“勾系一元二次方程”;
求证:关于x的“勾系一元二次方程”ax+
 cx+b=0必有实数根;
cx+b=0必有实数根;若x=1是“勾系一元二次方程”ax+
 cx+b=0的一个根,且四边形ACDE的周长是
cx+b=0的一个根,且四边形ACDE的周长是 ,求△ABC面积.
,求△ABC面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各计算题中,结果是零的是( )
A.(+3)﹣|﹣3|
B.|+3|+|﹣3|
C.(﹣3)﹣3
D. (﹣
(﹣  )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=
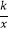 的图象如图所示,则二次函数y=﹣kx2﹣2x+
的图象如图所示,则二次函数y=﹣kx2﹣2x+ 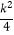 的图象大致为( )
的图象大致为( )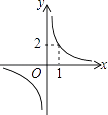
A.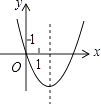
B.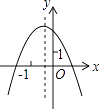
C.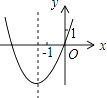
D.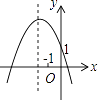
-
科目: 来源: 题型:
查看答案和解析>>【题目】某年级共有300名学生,为了解该年级学生在
 ,
, 两个体育项目上的达标情况,进行了抽样调査.过程如下,请补充完整.
两个体育项目上的达标情况,进行了抽样调査.过程如下,请补充完整.收集数据从该年级随机抽取30名学生进行测试,测试成绩(百分制)如下:
 项目 78 86 74 81 75 76 87 49 74 91 75 79 81 71 74 81 86 69 83 77 82 85 92 95 58 54 63 67 82 74
项目 78 86 74 81 75 76 87 49 74 91 75 79 81 71 74 81 86 69 83 77 82 85 92 95 58 54 63 67 82 74 项目 93 73 88 81 72 81 94 83 77 83 80 81 70 81 73 78 82 100 70 40 84 86 92 96 53 57 63 68 81 75
项目 93 73 88 81 72 81 94 83 77 83 80 81 70 81 73 78 82 100 70 40 84 86 92 96 53 57 63 68 81 75整理、描述数据
 项目的频数分布表
项目的频数分布表分组
划记
频数

—
1


2


2



8



5
(说明:成绩80分及以上为优秀,60~79分为基本达标,59分以下为不合格)
根据以上信息,回答下列问题:
(1)补全统计图、统计表;
(2)在此次测试中,成绩更好的项目是__________,理由是__________;
(3)假设该年级学生都参加此次测试,估计
 项目和
项目和 项目成绩都是优秀的人数最多为________人.
项目成绩都是优秀的人数最多为________人.
相关试题

