【题目】已知数轴上三点M,O,N对应的数分别为﹣2,0,4,点P为数轴上任意一点,其对应的数为x.
(1)如果点P到点M、点N的距离相等,那么x的值是多少?
(2)数轴上是否存在点P,使点P到点M、点N的距离之和是7?如果存在,求出x的值;如果不存在,请说明理由;
(3)如果点P以每秒钟6个单位长度的速度从点O向右运动时,点M和点N分别以每秒钟1个单位长度和每秒钟3个单位长度的速度也向右运动,且三点同时出发,那么经过几秒钟,点P到点M、点N的距离相等.
参考答案:
【答案】解:(1)∵数轴上三点M,O,N对应的数分别为﹣2,0,4,点P到点M、点N的距离相等,
∴点P是线段MN的中点,
∴x=(﹣2+4)÷2=1.
(2)存在;设P表示的数为x,
①当P在M点左侧时,PM+PN=7,
﹣2﹣x+4﹣x=7,
解得x=﹣2.5,
②当P点在N点右侧时,
x+2+x﹣4=7,
解得:x=4.5;
答:存在符合题意的点P,此时x=﹣2.5或4.5.
(3)设经过t秒点P到点M、点N的距离相等,则P点表示的数是6t,M点表示的数是﹣2+t,N点表示的数是4+3t,
由题意,得 PM=PN,
则6t﹣(﹣2+t)=|4+3t﹣6t|,
解得t=![]() .
.
答:经过![]() 秒钟,点P到点M、点N的距离相等.
秒钟,点P到点M、点N的距离相等.
【解析】(1)根据三点M,O,N对应的数,得出NM的中点为:x=(﹣3+1)÷2进而求出即可;
(2)根据P点在N点右侧或在M点左侧分别求出即可;
(3)设经过t秒点P到点M、点N的距离相等,则P点表示的数是6t,M点表示的数是﹣2+t,N点表示的数是4+3t,根据PM=PN建立方程,求解即可.
【考点精析】本题主要考查了数轴的相关知识点,需要掌握数轴是规定了原点、正方向、单位长度的一条直线才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明在大楼45米高(即PH=45米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:
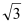 ,点P、H、B、C、A在同一个平面上,点H、B、C在同一条直线上,且PH⊥HC.
,点P、H、B、C、A在同一个平面上,点H、B、C在同一条直线上,且PH⊥HC.(1)山坡坡脚(即∠ABC)的度数等于 度;
(2)求A、B两点间的距离.(结果精确到1米,参考数据:
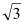 ≈1.732)
≈1.732)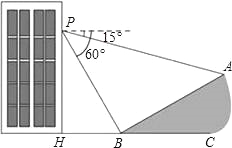
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:2(x2-2xy)-3(-xy-x2)-xy,其中x,y满足|x+1|+(y-2)2=0
-
科目: 来源: 题型:
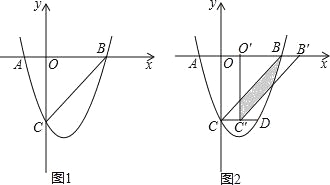
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴、y轴分别交于点A(﹣1,0),B(3,0)、C(0,﹣3)三点.
(1)直接写出抛物线的解析式 ;
(2)点D(2,m)在第一象限的抛物线上,连接BC、BD,试问,在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出点P点的坐标;如果不存在,请说明理由.
(3)如图2,在(2)的条件下,将△BOC沿x轴正方向以每秒1个单位长度的速度向右平移,记平移后的三角形为△B′O′C′,在平移过程中,△B′O′C′与△BCD重叠的面积记为S,设平移的时间为t秒(0≤t≤3),试求S与t之间的函数关系式?
-
科目: 来源: 题型:
查看答案和解析>>【题目】同学们都知道,|4-(-2)|表示4与-2的差的绝对值,实际上也可理解为4与-2两数在数轴上所对应的两点之间的距离;同理|x-3|也可理解为x与3两数在数轴上所对应的两点之间的距离,试探索并完成填空.
(1)求|4-(-2)|=______,|-3-5|=______;
(2)若|x-2|=5,则x=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小亮在上午8时,9时30分,10时,12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况,无意之中,他发现这四个时刻向日葵影子的长度各不相同,那么影子最长的时刻为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)40°26'+30°30'30″÷6;
(2)13°53'×3-32°5'31″.
相关试题

