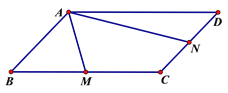
【题目】如图,在平行四边形ABCD中,M、N分别为BC、CD的中点,AM=1,AN=2,∠MAN=60°则AB的长为____________.
参考答案:
【答案】![]()
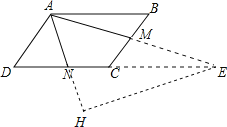
【解析】首先延长DC和AM交于E,过点E作EH⊥AN于点H,易证△ABM≌△ECM,则AM=EM=1,AN=2,且∠MAN=60°,求得AH,NH与EH的长,从而求得NE的长,则可求得答案.
解:(解法一)延长DC和AM交于E,过点E作EH⊥AN于点H,
∵ABCD为平行四边形
∴AB∥CE,
∴∠BAM=∠MEC,∠ABM=∠ECM,
∵M为BC的中点,
∴BM=MC,
∴△ABM≌△ECM,
∴AB=CD=CE,AM=EM=2,
∵N为DC的中点,
∴NE=3NC=![]() AB,即AB=
AB,即AB=![]() NE,
NE,
∵AN=2,AE=2AM=4,且∠MAN=60°,
∴∠AEH=30°,
∴AH=![]() AE=2,
AE=2,
∴EH=![]() ,
,
∴NH=AH-AN=2-1=1,
∴EN=![]() ,
,
∴AB=![]() .
.
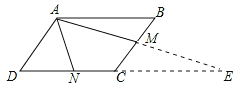
解法二:延长DC和AM交于E,根据平行四边形的性质可得出∠BAM=∠MEC,∠ABM=∠ECM,可证明△ABM≌△ECM,则AM=EM=2,由N为边DC的中点,得NR=3NC=1.5AB,AB=![]() NE,由余弦定理可解得EN,从而得出AB即可.
NE,由余弦定理可解得EN,从而得出AB即可.
解:延长DC和AM交于E,
∵ABCD为平行四边形
∴AB∥CE,
∴∠BAM=∠MEC,∠ABM=∠ECM,
∵M为BC的中点,
∴BM=MC,
∴△ABM≌△ECM,
∴AB=CD=CE,AM=EM=2,
∵N为DC的中点,
∴NE=3NC=1.5AB即AB=![]() NE,
NE,
∵AN=2,AE=2AM=4,且∠MAN=60°,
由余弦定理EN2=AE2+AN2-2AE×ANcos60°=16+1-2×4×![]() =13,
=13,
∴EN=![]() ,
,
∴AB=![]() .
.
故答案为: ![]() .
.
“点睛”本题考查了平行线的性质、勾股定理以及三角形的中位线定理,是中考常见的题型,难度偏大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,直线
中,直线 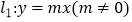 与直线
与直线 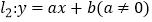 相交于点A(2,4),直线
相交于点A(2,4),直线 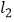 与x轴交于点B(6,0).
与x轴交于点B(6,0).
(1)分别求直线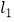 和
和 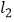 的表达式;
的表达式;
(2)过动点P(0,n)且垂直于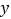 轴的直线与
轴的直线与 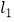 ,
, 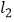 的交点分别为C , D , 当点C 位于点D左方时,请直接写出n的取值范围.
的交点分别为C , D , 当点C 位于点D左方时,请直接写出n的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形
 中,
中, 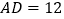 ,
,  ,点
,点 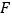 是
是 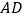 边上一点,过点
边上一点,过点 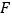 作
作  ,交射线
,交射线 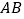 于点
于点 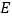 ,交射线
,交射线 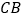 于点
于点  .
.
(1)如图1,若 ,则
,则 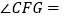 度;
度;
(2)当以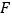 ,
,  ,
, 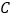 为顶点的三角形是等边三角形时,依题意在图2中补全图形并求
为顶点的三角形是等边三角形时,依题意在图2中补全图形并求  的长;
的长;
(3)过点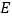 作
作  ∥
∥ 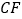 交射线
交射线 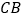 于点
于点 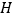 ,请探究:当
,请探究:当  为何值时,以
为何值时,以 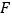 ,
, 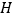 ,
, 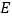 ,
, 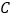 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=(x﹣1)2﹣4的图象先向左平移2个单位,再向上平移3个单位,所得函数解析式为( )
A.y=(x﹣1)2+1
B.y=(x﹣3)2﹣1
C.y=(x+1)2﹣1
D.y=(x+2)2+3 -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校准备开展“阳光体育活动”,决定开设以下体育活动项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项,为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并将通过获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题:

(1)这次活动一共调查了多少名学生?
(2)补全条形统计图;
(3)在扇形统计图中,选择篮球项目的人数所在扇形的圆心角等于多少度?
(4)若该学校有1500人,请你估计该学校选择足球项目的学生人数;
(5)九(1)班从参加乒乓球活动的学生中挑选四名优秀学生张杰、吴元、金贤、郝涛,随机选取两人为一组,另两人为一组,进行男子双打对抗训练,准备参加县乒乓球比赛.用树状图或列表法求吴元与金贤恰好分在同一组的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下为说法中正确的个数是( )
①射线AB与射线BA是同一条射线;②两点确定一条直线;③对顶角相等;④不相交的两条直线叫做平行线;⑤过一点有只有一条直线与这条直线平行.
A. 1
B. 2
C. 3
D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的( ).
A.在同一平面内,两条直线的位置只有两种:相交和垂直.
B.有且只有一条直线垂直于已知直线.
C.如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
D.从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离.
相关试题

