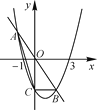
【题目】已知抛物线y＝ax2＋bx－3经过(－1，0)，(3，0)两点，与y轴交于点C，直线y＝kx与抛物线交于A，B两点．

(1)写出点C的坐标并求出此抛物线的解析式；

(2)当原点O为线段AB的中点时，求k的值及A，B两点的坐标；

(3)是否存在实数k使得△ABC的面积为？若存在，求出k的值；若不存在，请说明理由．

参考答案：

【答案】（1）y=x2﹣2x﹣3；（2）当原点O为线段AB的中点时，k的值为﹣2，点A的坐标为（﹣，2），点B的坐标为（，﹣2）．（3）不存在，理由详见解析.

【解析】试题分析：（1）令x=0求出y值即可得出C点的坐标，又有点（﹣1，0）、（3，0），利用待定系数法求抛物线的解析式即可；（2）将正比例函数解析式代入抛物线解析式中，找出关于x的一元二次方程，根据根与系数的关系即可得出“xA+xB=2+k，xAxB=﹣3”，结合点O为线段AB的中点即可得出xA+xB=2+k=0，由此得出k的值，将k的值代入一元二次方程中求出xA、xB，在代入一次函数解析式中即可得出点A、B的坐标；（3）假设存在，利用三角形的面积公式以及（2）中得到的“xA+xB=2+k，xAxB=﹣3”，即可得出关于k的一元二次方程，结合方程无解即可得出假设不成立，从而得出不存在满足题意的k值．

试题解析：（1）令抛物线y=ax2+bx﹣3中x=0，则y=﹣3，

∴点C的坐标为（0，﹣3）．

∵抛物线y=ax2+bx﹣3经过（﹣1，0），（3，0）两点，

∴有，解得：，

∴此抛物线的解析式为y=x2﹣2x﹣3．

（2）将y=kx代入y=x2﹣2x﹣3中得：kx=x2﹣2x﹣3，

整理得：x2﹣（2+k）x﹣3=0，

∴xA+xB=2+k，xAxB=﹣3．

∵原点O为线段AB的中点，

∴xA+xB=2+k=0，

解得：k=﹣2．

当k=﹣2时，x2﹣（2+k）x﹣3=x2﹣3=0，

解得：xA=﹣，xB=．

∴yA=﹣2xA=2，yB=﹣2xB=2．

故当原点O为线段AB的中点时，k的值为﹣2，点A的坐标为（﹣，2），点B的坐标为（，﹣2）．

（3）假设存在．

由（2）可知：xA+xB=2+k，xAxB=﹣3，

S△ABC=OC|xA﹣xB|=×3×=，

∴（2+k）2﹣4×（﹣3）=10，即（2+k）2+2=0．

∵（2+k）2非负，无解．

故假设不成立．

所以不存在实数k使得△ABC的面积为．

关闭