【题目】如图1,抛物线y=x2﹣2x+k与x轴交于点A、B两点,与y轴交于点C(0,﹣3)(图2,图3为解答备用图).
(1)k= ,点A的坐标为 ,点B的坐标为 ;
(2)设抛物线y=x2﹣2x+k的顶点为M,求四边形ABMC的面积;
(3)在x轴下方的抛物线上是否存在一点D,使四边形ABDC的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)﹣3,(﹣1,0),(3,0);
(2)S四边形ABMC=9;
(3)当m=![]() 时,S四边形ABDC最大,此时D(
时,S四边形ABDC最大,此时D(![]() ,﹣
,﹣![]() ).
).
【解析】
试题分析:(1)将C点坐标代入抛物线解析式可求k的值,由抛物线解析式求A,B两点坐标;
(2)根据A、B、M、N四点坐标,将四边形分割为两个三角形和一个梯形求面积;
(3)只要使△DBC面积最大即可,由此求D点坐标;
试题解析:(1)将C(0,﹣3)代入抛物线y=x2﹣2x+k中,得k=﹣3,
∴抛物线解析式为y=x2﹣2x﹣3,
令y=0,得x=﹣1或3,
∴A(﹣1,0),B(3,0);
故答案为﹣3,(﹣1,0),(3,0);
(2)如图(1),
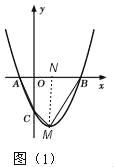
过M点作MN⊥AB,垂足为N,
由y=x2﹣2x﹣3=(x﹣1)2﹣4,可知M(1,﹣4),
∴S四边形ABMC=S△ACO+S梯形OCMN+S△BMN=![]() ×1×3+
×1×3+![]() ×(3+4)×1+
×(3+4)×1+![]() ×(3﹣1)×4=9;
×(3﹣1)×4=9;
(3)存在,如图(2),
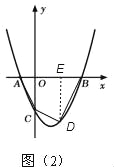
设D(m,m2﹣2m﹣3),
过D点作DE⊥AB,垂足为E,则
S四边形ABDC=S△ACO+S梯形OCDE+S△BDE
=![]() ×1×3+
×1×3+![]() ×[3﹣(m2﹣2m﹣3)]×m+
×[3﹣(m2﹣2m﹣3)]×m+![]() ×(3﹣m)×[﹣(m2﹣2m﹣3)]
×(3﹣m)×[﹣(m2﹣2m﹣3)]
=﹣![]() m2+
m2+![]() m+6,
m+6,
∵﹣![]() <0,
<0,
∴当m=﹣![]() =
=![]() 时,S四边形ABDC最大,此时D(
时,S四边形ABDC最大,此时D(![]() ,﹣
,﹣![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】“蜀”你最好!疫情发生以来,四川累计派出1463名医护人员支援湖北.数字1463用科学记数法表示为( )
A.0.1463×104B.1.463×103C.14.63×102D.1.463×104
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.

-
科目: 来源: 题型:
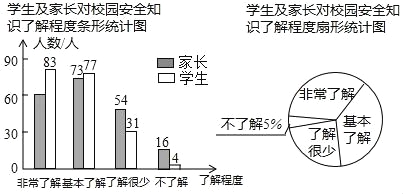
查看答案和解析>>【题目】“校园安全”受到全社会的广泛关注,某校政教处对部分学生及家长就校园安全知识的了解程度,进行了随机抽样调查,并绘制成如图所示的两幅统计图,请根据统计图中的信息,解答下列问题:
(1)参与调查的学生及家长共有 人;
(2)在扇形统计图中,“基本了解”所对应的圆心角的度数是 度;
(3)在条形统计图中,“非常了解”所对应的家长人数是 人;
(4)若全校有1200名学生,请你估计对“校园安全”知识达到“非常了解”和“基本了解”的学生共有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,是方程的个数为( )
(1)﹣3﹣3=﹣7;(2)3x﹣5=2x+1;(3)2x+6;(4)x﹣y=0;(5)a+b>3;(6)a2+a﹣6=0.
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)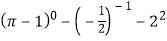
(2)(p﹣q)4÷(q﹣p)3(p﹣q)2
(3)aa2a3+(﹣2a3)2﹣a8÷a2
(4)(﹣2x)2(x2)3÷(﹣x)2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个等腰三角形的两边长是3cm和7cm,则它的周长为( )
A. 13cm B. 17cm C. 13或17cm D. 10cm
相关试题

