【题目】把Rt△ABC和Rt△DEF按如图(1)摆放(点C与E重合),点B、C(E)、F在同一条直线上.已知:∠ACB=∠EDF=90°,∠DEF=45°,AC=8cm,BC=6cm,EF=10cm.如图(2),△DEF从图(1)的位置出发,以1cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点A出发,以2cm/s的速度沿AB向点B匀速移动;当点P移动到点B时,点P停止移动,△DEF也随之停止移动.DE与AC交于点Q,连接PQ,设移动时间为t(s). 
(1)用含t的代数式表示线段AP和AQ的长,并写出t的取值范围;
(2)连接PE,设四边形APEQ的面积为y(cm2),试探究y的最大值;
(3)当t为何值时,△APQ是等腰三角形.
参考答案:
【答案】
(1)解:AP=2t
∵∠EDF=90°,∠DEF=45°,
∴∠CQE=45°=∠DEF,
∴CQ=CE=t,
∴AQ=8﹣t,
t的取值范围是:0≤t≤5;
(2)解:过点P作PG⊥x轴于G,可求得AB=10,SinB= ![]() ,PB=10﹣2t,EB=6﹣t,
,PB=10﹣2t,EB=6﹣t,

∴PG=PBSinB= ![]() (10﹣2t)
(10﹣2t)
∴y=S△ABC﹣S△PBE﹣S△QCE= ![]() =
= ![]()
∴当 ![]() (在0≤t≤5内),y有最大值,y最大值=
(在0≤t≤5内),y有最大值,y最大值= ![]() (cm2)
(cm2)
(3)解:若AP=AQ,则有2t=8﹣t解得: ![]() (s)
(s)
若AP=PQ,如图①:过点P作PH⊥AC,则AH=QH= ![]() ,PH∥BC
,PH∥BC

∴△APH∽△ABC,
∴ ![]() ,
,
即 ![]() ,
,
解得: ![]() (s)
(s)
若AQ=PQ,如图②:过点Q作QI⊥AB,则AI=PI= ![]() AP=t
AP=t

∵∠AIQ=∠ACB=90°∠A=∠A,
∴△AQI∽△ABC
∴ ![]() 即
即 ![]() ,
,
解得: ![]() (s)
(s)
综上所述,当 ![]() 或
或 ![]() 或
或 ![]() 时,△APQ是等腰三角形.
时,△APQ是等腰三角形.
【解析】(1)根据题意以及直角三角形性质表达出CQ、AQ,从而得出结论,(2)作PG⊥x轴,将四边形的面积表示为S△ABC﹣S△BPE﹣S△QCE即可求解,(3)根据题意以及三角形相似对边比例性质即可得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38,
 ≈1.73,精确到个位)
≈1.73,精确到个位) 
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=kx+b与反比例函数y=
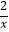 (x<0)的图象交于点A(﹣1,m),与x轴交于点B(1,0)
(x<0)的图象交于点A(﹣1,m),与x轴交于点B(1,0) 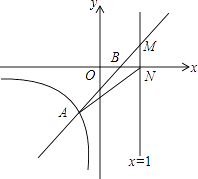
(1)求m的值;
(2)求直线AB的解析式;
(3)若直线x=t(t>1)与直线y=kx+b交于点M,与x轴交于点N,连接AN,S△AMN= ,求t的值.
,求t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
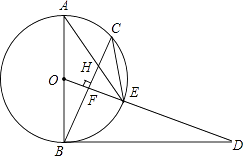
(1)求证:BD是⊙O的切线;
(2)求证:CE2=EHEA;
(3)若⊙O的半径为5,sinA= ,求BH的长.
,求BH的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为1的正方形ABCD,点M从点A出发以每秒1个单位长度的速度向点B运动,点N从点A出发以每秒3个单位长度的速度沿A→D→C→B的路径向点B运动,当一个点到达点B时,另一个点也随之停止运动,设△AMN的面积为s,运动时间为t秒,则能大致反映s与t的函数关系的图象是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,将△ABC绕点C按顺时针方向旋转n度后,得到△EDC,此时,点D在AB边上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(2017﹣
 )0×
)0× 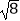 ﹣(
﹣(  )﹣1﹣4cos45°.
)﹣1﹣4cos45°.
相关试题

