【题目】直线y=kx+b与反比例函数y= ![]() (x<0)的图象交于点A(﹣1,m),与x轴交于点B(1,0)
(x<0)的图象交于点A(﹣1,m),与x轴交于点B(1,0) 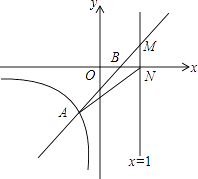
(1)求m的值;
(2)求直线AB的解析式;
(3)若直线x=t(t>1)与直线y=kx+b交于点M,与x轴交于点N,连接AN,S△AMN= ![]() ,求t的值.
,求t的值.
参考答案:
【答案】
(1)解:将点A(﹣1,m)代入y= ![]() ,得:m=﹣2;
,得:m=﹣2;
(2)解:由(1)知点A坐标为(﹣1,﹣2),
将点A(﹣1,﹣2)、B(1,0)代入y=kx+b,
得: ![]() ,
,
解得: ![]() ,
,
∴直线AB的解析式为:y=x﹣1;
(3)解:当x=t时,y=t﹣1,
∴点M坐标为(t,t﹣1),点N坐标为(t,0),
∵S△AMN= ![]() ,
,
∴ ![]() ×(t﹣1)(t+1)=
×(t﹣1)(t+1)= ![]() ,
,
解得:t=2或t=﹣2(舍),
∴t=2.
【解析】(1)将点A坐标代入y= ![]() 可得m的值;(2)将点A、B坐标代入y=kx+b可得关于k、b的方程,解方程求出k、b的值,可得直线解析式;(3)根据直线直线x=t与直线y=kx+b交于点M、与x轴交于点N表示出M、N的坐标,由S△AMN=
可得m的值;(2)将点A、B坐标代入y=kx+b可得关于k、b的方程,解方程求出k、b的值,可得直线解析式;(3)根据直线直线x=t与直线y=kx+b交于点M、与x轴交于点N表示出M、N的坐标,由S△AMN= ![]() 可得关于t的方程,解方程可得t的值.
可得关于t的方程,解方程可得t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,∠A=30°.

(1)用尺规作图作AB边上的垂直平分线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明)
(2)连接BD,求证:DE=CD. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A篮球、B乒乓球、C跳绳、D踢毽子,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:

(1)这次被调查的学生共有人;
(2)请你将条形统计图补充完成;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答). -
科目: 来源: 题型:
查看答案和解析>>【题目】为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38,
 ≈1.73,精确到个位)
≈1.73,精确到个位) 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
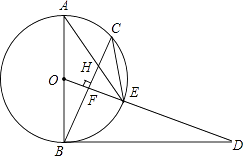
(1)求证:BD是⊙O的切线;
(2)求证:CE2=EHEA;
(3)若⊙O的半径为5,sinA= ,求BH的长.
,求BH的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】把Rt△ABC和Rt△DEF按如图(1)摆放(点C与E重合),点B、C(E)、F在同一条直线上.已知:∠ACB=∠EDF=90°,∠DEF=45°,AC=8cm,BC=6cm,EF=10cm.如图(2),△DEF从图(1)的位置出发,以1cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点A出发,以2cm/s的速度沿AB向点B匀速移动;当点P移动到点B时,点P停止移动,△DEF也随之停止移动.DE与AC交于点Q,连接PQ,设移动时间为t(s).

(1)用含t的代数式表示线段AP和AQ的长,并写出t的取值范围;
(2)连接PE,设四边形APEQ的面积为y(cm2),试探究y的最大值;
(3)当t为何值时,△APQ是等腰三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为1的正方形ABCD,点M从点A出发以每秒1个单位长度的速度向点B运动,点N从点A出发以每秒3个单位长度的速度沿A→D→C→B的路径向点B运动,当一个点到达点B时,另一个点也随之停止运动,设△AMN的面积为s,运动时间为t秒,则能大致反映s与t的函数关系的图象是( )

A.
B.
C.
D.
相关试题

