【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣8,3),B(﹣4,0),C(﹣4,3),∠ABC=α°.抛物线y=![]() x2+bx+c经过点C,且对称轴为x=﹣
x2+bx+c经过点C,且对称轴为x=﹣![]() ,并与y轴交于点G.
,并与y轴交于点G.
(1)求抛物线的解析式及点G的坐标;
(2)将Rt△ABC沿x轴向右平移m个单位,使B点移到点E,然后将三角形绕点E顺时针旋转α°得到△DEF.若点F恰好落在抛物线上.①求m的值;
②连接CG交x轴于点H,连接FG,过B作BP∥FG,交CG于点P,求证:PH=GH.

参考答案:
【答案】(1)y=![]() x2+
x2+![]() x
x![]() ,点G(0,-
,点G(0,-![]() );(2)①
);(2)①![]() ;②证明见解析.
;②证明见解析.
【解析】试题分析:(1)把点C坐标代入y=![]() x2+bx+c得一方程,用对称轴公式得另一方程,组成方程组求出解析式,并求出G点的坐标;(2)①作辅助线,构建直角△DEF斜边上的高FM,利用直角三角形的面积相等和勾股定理可表示F的坐标,根据点F在抛物线上,列方程求出m的值;②F点和G点坐标已知,可以求出直线FG的方程,那么FG和x轴的交点坐标(设为Q)可以知道,C点坐标已知,CG的方程也可以求出,那么H点坐标可以求出,可以证明△BPH和△QGH全等.
x2+bx+c得一方程,用对称轴公式得另一方程,组成方程组求出解析式,并求出G点的坐标;(2)①作辅助线,构建直角△DEF斜边上的高FM,利用直角三角形的面积相等和勾股定理可表示F的坐标,根据点F在抛物线上,列方程求出m的值;②F点和G点坐标已知,可以求出直线FG的方程,那么FG和x轴的交点坐标(设为Q)可以知道,C点坐标已知,CG的方程也可以求出,那么H点坐标可以求出,可以证明△BPH和△QGH全等.
试题解析:(1)根据题意得: 
解得: 
∴抛物线的解析式为:y=![]() x2+
x2+![]() x﹣
x﹣![]() ,点G(0,﹣
,点G(0,﹣![]() );
);
(2)①过F作FM⊥y轴,交DE于M,交y轴于N,
由题意可知:AC=4,BC=3,则AB=5,FM=![]() ,
,
∵Rt△ABC沿x轴向右平移m个单位,使B点移到点E,
∴E(﹣4+m,0),OE=MN=4﹣m,FN=![]() ﹣(4﹣m)=m﹣
﹣(4﹣m)=m﹣![]() ,
,
在Rt△FME中,由勾股定理得:EM= =
=![]() ,
,
∴F(m﹣![]() ,
, ![]() ),
),
∵F抛物线上,
∴![]() =
=![]() (m﹣
(m﹣![]() )2+
)2+![]() (m﹣
(m﹣![]() )﹣
)﹣![]() ,
,
5m2﹣8m﹣36=0,
m1=﹣2(舍),![]() ;
;
②F(![]() ,
, ![]() ),
),
∴F(2, ![]() ),
),
易求得FG的解析式为:y=![]() x﹣
x﹣![]() ,
,
CG解析式为:y=﹣![]() x﹣
x﹣![]() ,
,
∴![]() x﹣
x﹣![]() =0,x=1,则Q(1,0),
=0,x=1,则Q(1,0),
﹣![]() x﹣
x﹣![]() =0,x=﹣1.5,则H(﹣1.5,0),
=0,x=﹣1.5,则H(﹣1.5,0),
∴BH=4﹣1.5=2.5,HQ=1.5+1=2.5,
∴BH=QH,
∵BP∥FG,
∴∠PBH=∠GQH,∠BPH=∠QGH,
∴△BPH≌△QGH,
∴PH=GH.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列多边形中,内角和是外角和的两倍的是( )
A. 四边形 B. 五边形 C. 六边形 D. 八边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的B′点,AE是折痕.
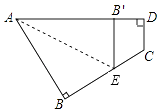
(1)试判断B′E与DC的位置关系,并说明理由;
(2)如果∠C=128°,求∠AEB的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了打造区域中心城市,实现跨越式发展,我市新区建设正按投资计划有序推进.新区建设工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m3 , 现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如表:
租金(单位:元/台时)
挖掘土石方量(单位:m3/台时)
甲型挖掘机
100
60
乙型挖掘机
120
80
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有几种不同的租用方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面的内容,再解决问题,
例题:若m2+2mn+2n2﹣6n+9=0,求m和n的值.
解:∵m2+2mn+2n2﹣6n+9=0
∴m2+2mn+n2+n2﹣6n+9=0
∴(m+n)2+(n﹣3)2=0
∴m+n=0,n﹣3=0
∴m=﹣3,n=3
问题(1)若x2+2y2﹣2xy+4y+4=0,求xy的值.
(2)已知a,b,c是△ABC的三边长,满足a2+b2=10a+8b﹣41,且c是△ABC中最长的边,求c的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)学校组织学生参加综合实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如下表所示:
第1天
第2天
第3天
第4天
售价x(元/双)
150
200
250
300
销售量y(双)
40
30
24
20
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价定为多少元?
相关试题

