Question

【题目】如图，在平面直角坐标系xOy中，点C的坐标为（4，0），一次函数 的图像分别交x轴、y轴于点A、点B.

（1）若点D是直线AB在第一象限内的点，且BD＝BC，试求出点D的坐标.
（2）在⑴的条件下，若点Q是坐标轴上的一个动点，试探索在第一象限是否存在另一个点P，使得以B、D、P、Q为顶点的四边形是菱形（BD为菱形的一边）？若存在，请直接写出点P的坐标；若不存在，请说明理由．

Answer 1

【答案】
（1）解：如图1，设点D（3a，4a+3），
过点D作DE⊥y轴于E，把x=0代入y= x+3中，得，y=3，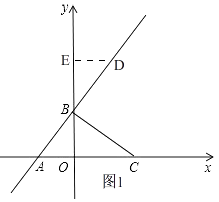

∴OB=3，
∴BE=OE-OB=4a+3-3=4a，BC= =5，
在Rt△BED中，根据勾股定理得，（3a）2+（4a）2=52 ，
∴a=±1，
∵点D在第一象限，
∴a=1，
∴D（3，7）
（2）解：由（1）知，BD=BC=5，
①当点Q在y轴上时，
设Q（0，q），
∵使得以B，D，P，Q为顶点的四边形是菱形（BD为菱形的一边），且点P在第一象限内，
即：四边形BDPQ是菱形，
∴PQ∥BD，DP∥BQ，
∴点P的横坐标为3，
∵四边形BDPQ是菱形，
∴BQ=BD=5，
∵B（0，3），
∴Q（0，8）或（0，-2），
Ⅰ、当点Q（0，8）时，
∵直线BD的解析式为y= x+3，
∴直线PQ的解析式为y= x+8，
当x=3时，y=12，
∴P（3，12），
Ⅱ、点Q（0，-2）时，
∵直线BD的解析式为y= x+3，
∴直线PQ的解析式为y= x-2，
当x=3时，y=2，
∴P（3，2），
②当点Q在x轴上时，
设Q（m，0），），
∵使得以B，D，P，Q为顶点的四边形是菱形（BD为菱形的一边），且点P在第一象限内，
即：四边形BDPQ是菱形，
∴BQ=BD=5，
∵OB=3，
∴OQ=4，
∴Q（-4，0）或（4，0）
Ⅰ、当Q（-4，0）时，∵一次函数y= x+3的图象交x轴于点A，
∴A（- ，0），
∴点Q在点A的左侧，
∴点P在第二象限内，不符合题意，舍去，
Ⅱ、当点Q（4，0）时，∵四边形BDPQ是菱形，
∴BQ∥DP，PQ∥BD，
∵直线BD的解析式为y= x+3，
∴设直线PQ的解析式为y= x+b，
∴ ×4+b=0，
∴b=- ，
∴直线PQ的解析式为y= x- ①，
∵B（0，3），Q（4，0），
∴直线BQ的解析式为y=- x+3，
∵D（3，7），
∴直线DP的解析式为y=- x+ ②，
联立①②解得，x=7，y=4，
∴P（7，4），
即：满足条件的点P的坐标为（3，12）、（3，2）、（7，4）．
【解析】（1）过点D作DE⊥y轴于E，先求出直线AB与y轴的交点坐标，再根据勾股定理求出BC的长，然后在Rt△BED中用勾股定理建立方程求出a的值，就可求得点D的坐标。
（2）分两种情况讨论：①当点Q在y轴上时，利用菱形的性质求出BQ=5，再求出点Q的坐标为（0，8）或（0，-2），然后利用菱形的性质求出当点Q为（0，8）和（0，-2）时的点P的坐标；②当点Q在x轴上时，先求出点Q的坐标为（-4，0）或（4，0），然后利用菱形的性质分别求出点Q的坐标为（-4，0）和（4，0）时的点P的坐标。