【题目】在平面直角坐标系中,O是坐标原点,ABCD的顶点A的坐标为(﹣2,0),点D的坐标为(0,2![]() ),点B在x轴的正半轴上,点E为线段AD的中点.
),点B在x轴的正半轴上,点E为线段AD的中点.


(Ⅰ)如图1,求∠DAO的大小及线段DE的长;
(Ⅱ)过点E的直线l与x轴交于点F,与射线DC交于点G.连接OE,△OEF′是△OEF关于直线OE对称的图形,记直线EF′与射线DC的交点为H,△EHC的面积为3![]() .
.
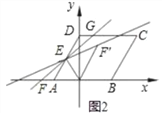
①如图2,当点G在点H的左侧时,求GH,DG的长;
②当点G在点H的右侧时,求点F的坐标(直接写出结果即可).
参考答案:
【答案】(Ⅰ)∠DAO=60°,DE=2; (Ⅱ)①GH=6,DG=﹣3+![]() ;②F(﹣5﹣
;②F(﹣5﹣![]() ,0).
,0).
【解析】解:(Ⅰ)∵A(﹣2,0),D(0,2![]() )∴AO=2,DO=2
)∴AO=2,DO=2![]() ,∴tan∠DAO=
,∴tan∠DAO=![]() =
=![]() ,
,
∴∠DAO=60°,∴∠ADO=30°,∴AD=2AO=4,∵点E为线段AD中点,∴DE=2;
(Ⅱ)①如图2,

过点E作EM⊥CD,∴CD∥AB,∴∠EDM=∠DAB=60°,∴EM=DEsin60°=![]() ,∴GH=6,
,∴GH=6,
∵CD∥AB,∴∠DGE=∠OFE,
∵△OEF′是△OEF关于直线OE的对称图形,∴△OEF′≌△OEF,∴∠OFE=∠OF′E,
∵点E是AD的中点,∴OE=![]() AD=AE,
AD=AE,
∵∠EAO=60°,∴△EAO是等边三角形,∴∠EOA=60°,∠AEO=60°,
∵△OEF′≌△OEF,∴∠EOF′=∠EOA=60°,
∴∠EOF′=∠AEO,∴AD∥OF′,∴∠OF′E=∠DEH,∴∠DEH=∠DGE,
∵∠DEH=∠EDG,∴△DHE∽△DEG,∴![]() ,∴DE2=DG×DH,
,∴DE2=DG×DH,
设DG=x,则DH=x+6,∴4=x(x+6),∴x1=﹣3+![]() ,x2=﹣3﹣
,x2=﹣3﹣![]() ,∴DG=﹣3+
,∴DG=﹣3+![]() .
.
②如图3,

过点E作EM⊥CD,∴CD∥AB,∴∠EDM=∠DAB=60°,∴EM=DEsin60°=![]() ,∴GH=6,
,∴GH=6,
∵CD∥AB,∴∠DHE=∠OFE,
∵△OEF′是△OEF关于直线OE的对称图形,∴△OEF′≌△OEF,∴∠OFE=∠OF′E,
∵点E是AD的中点,∴OE=![]() AD=AE,
AD=AE,
∵∠EAO=60°,∴△EAO是等边三角形,∴∠EOA=60°,∠AEO=60°,
∵△OEF′≌△OEF,∴∠EOF′=∠EOA=60°,∴∠EOF′=∠AEO,∴AD∥OF′,
∴∠OF′E=∠DEH,∴∠DEG=∠DHE,
∵∠DEG=∠EDH,∴△DGE∽△DEH,∴![]() ,∴DE2=DG×DH,
,∴DE2=DG×DH,
设DH=x,则DG=x+6,∴4=x(x+6),∴x1=﹣3+![]() ,x2=﹣3﹣
,x2=﹣3﹣![]() ,
,
∴DH=﹣3+![]() .∴DG=3+
.∴DG=3+![]() ∴DG=AF=3+
∴DG=AF=3+![]() ,∴OF=5+
,∴OF=5+![]() ,∴F(﹣5﹣
,∴F(﹣5﹣![]() ,0).
,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中是随机事件的是( )
A.校运会上立定跳远成绩为10米
B.在只装有5个红球的袋中,摸出一个红球
C.慈溪市明年五一节是晴天
D.在标准大气压下,气温3°C 时,冰熔化为水
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察图形,回答下列各题:
(1)图A中,共有____对对顶角;
(2)图B中,共有____对对顶角;
(3)图C中,共有____对对顶角;
(4)探究(1)--(3)各题中直线条数与对顶角对数之间的关系,若有n条直线相交于一点,则可形成________对对顶角;

-
科目: 来源: 题型:
查看答案和解析>>【题目】x与y差的平方,列代数式正确的是( )
A.x﹣y2B.(x﹣y)2C.x2﹣yD.x2﹣y2
-
科目: 来源: 题型:
查看答案和解析>>【题目】把9-(+4)-(-7)+(-3)写成省略加号的和的形式为( )
A.9-4+7+3B.9+4-7-3C.9-4+7-3D.9-4-7+3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,BD垂直平分AC,垂足为点F,E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC.

(1)求证:四边形ABDE是平行四边形;
(2)如果DA平分∠BDE,AB=5,AD=6,求AC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是真命题的是( )
A.在同圆或等圆中,等弧所对的圆周角相等
B.平分弦的直径垂直于弦
C.在同圆或等圆中,等弦所对的圆周角相等
D.三角形外心是三条角平分线的交点
相关试题

