Question

【题目】某市开展一项自行车旅游活动，线路需经A，B，C，D四地，如图，其中A，B，C三地在同一直线上，D地在A地北偏东30°方向，在C地北偏西45°方向，C地在A地北偏东75°方向．且BC=CD=20km，问沿上述线路从A地到D地的路程大约是多少？（最后结果保留整数，参考数据：sin15°≈0.25，cos15°≈0.97，tan15°≈0.27， ）

Answer 1

【答案】解：由题意可知∠DCA=180°﹣75°﹣45°=60°，

∵BC=CD，

∴△BCD是等边三角形．

过点B作BE⊥AD，垂足为E，如图所示：

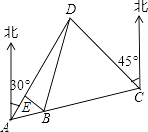
由题意可知∠DAC=75°﹣30°=45°，

∵△BCD是等边三角形，

∴∠DBC=60° BD=BC=CD=20km，

∴∠ADB=∠DBC﹣∠DAC=15°，

∴BE=sin15°BD≈0.25×20≈5m，

∴AB= = ≈7m，

∴AB+BC+CD≈7+20+20≈47m．

答：从A地跑到D地的路程约为47m．

【解析】过点B作BE⊥AD，垂足为E，先求出∠DCA=60°，然后再判断出BC=CD，从而可得到△BCD是等边三角形，然后再求出∠DAC的度数，利用三角函数求出AB的长，最后，再求得AB+BC+CD的长即可.